
分析 (1)由题意画出图形,求出M点关于直线y=-x的对称点,则a可求,再由△MF1F2为正三角形列式求得c,结合隐含条件求得b,则椭圆方程可求,
(2)设直线PB的方程可设为x=ky+4,联立方程组,设B(x1,y1),E(x2,y2),则A(x1,-y1),根据韦达定理可得y1+y2=-$\frac{16k}{2{k}^{2}+3}$,y1•y2=$\frac{24}{2{k}^{2}+3}$,由此能够证明直线AE恒过定点(1,0).
解答 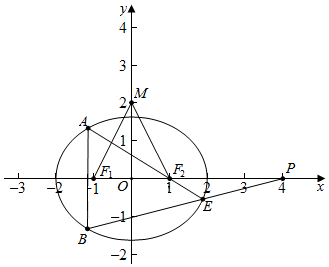 解:(1)如图,点M(0,2)关于直线y=-x的对称点为(-2,0),
解:(1)如图,点M(0,2)关于直线y=-x的对称点为(-2,0),
∵(-2,0)在椭圆上,∴a=2,
又△MF1F2为正三角形,
∴tan30°=$\frac{c}{2}$,c=2tan30°=$\frac{2\sqrt{3}}{3}$,
∴b2=a2-c2=4-$\frac{4}{3}$=$\frac{8}{3}$,
∴椭圆C的方程$\frac{{x}^{2}}{4}$+$\frac{3{y}^{2}}{8}$=1;
(2)∵P(4,0),
∴直线PB的方程可设为x=ky+4,
由$\left\{\begin{array}{l}{x=ky+4}\\{2{x}^{2}+3{y}^{2}=8}\end{array}\right.$,
得(2k2+3)y2+16ky+24=0,
∵△>0,
∴k2>$\frac{9}{2}$.
设B(x1,y1),E(x2,y2),则A(x1,-y1),
∴y1+y2=-$\frac{16k}{2{k}^{2}+3}$,y1•y2=$\frac{24}{2{k}^{2}+3}$
直线AE:y+y1=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$(x-x1),
∵x1y2+x2y1=2ky1y2+4(y1+y2)=$\frac{48k}{2{k}^{2}+3}$-$\frac{64k}{2{k}^{2}+3}$=-$\frac{16k}{2{k}^{2}+3}$=y1+y2,
∴直线AE:y+y1=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$(x-x1),即为y=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}$(x-1)恒过定点(1,0).
∴AE恒过定点(1,0).
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${A}_{100-n}^{80}$ | B. | ${A}_{100-n}^{21-n}$ | C. | ${A}_{100-n}^{79}$ | D. | ${A}_{100}^{21-n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
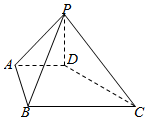 如图,PD⊥平面ABCD,DC⊥AD,BC∥AD,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,DC⊥AD,BC∥AD,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,直角坐标系x′Oy所在的平面为β,直角坐标系xOy所在的平面为α,且二面角α-y轴-β的大小等于30°.已知β内的曲线C′的方程是3(x-2$\sqrt{3}$)2+4y2-36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是(x-3)2+y2=9.
如图,直角坐标系x′Oy所在的平面为β,直角坐标系xOy所在的平面为α,且二面角α-y轴-β的大小等于30°.已知β内的曲线C′的方程是3(x-2$\sqrt{3}$)2+4y2-36=0,则曲线C′在α内的射影在坐标系xOy下的曲线方程是(x-3)2+y2=9.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 210-1 | B. | 212-1 | C. | 310-1 | D. | 332-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com