
���� ��1�����õȲ�������ȱ����е�ͨ�ʽ���ɵó���
��2����pn=$\left\{\begin{array}{l}{a_n}��n=2k-1��k��{N^*}\\{b_n}��n=2k��k��{N^*}\end{array}$���ɵ�����{pn}��ǰ2n���S2n=��a1+a3+��+a2n-1��+��b2+b4+��+b2n��=$\frac{2}{3}��{4}^{n}$-$\frac{2}{3}$-2n2-12n��n=1��2��3ʱ��S2n��0��n��4ʱ������S2n��0�����ɵó���
����S1=2��S2=-12��S3=-4��S4=-22��S5=10��S6=-12��S7=116���ɢٿ�֪��ʹ�õ�n��4ʱ������S2n��0��������an=2n��0�����n��8ʱ������Sn��0����Sn�������������ɵó���
��� �⣺��1����ȱ�����{an}�Ĺ���Ϊq��0���Ȳ�����{bn}�Ĺ���Ϊd����a1a2a3=64��b1+b2+b3=-42��6a1+b1=2a3+b3=0��
��${a}_{2}^{3}$=64��3b2=-42��$\frac{6{a}_{2}}{q}$+b2-d=2a2q+b2+d=0��
�������a2=4��b2=-14��q=2��d=-2��
��an=${a}_{2}{q}^{n-2}$=4��2n-2=2n��bn=b2+��n-2��d=-14-2��n-2��=-2n-10��
��2���١�pn=$\left\{\begin{array}{l}{a_n}��n=2k-1��k��{N^*}\\{b_n}��n=2k��k��{N^*}\end{array}$��
����{pn}��ǰ2n���S2n=��a1+a3+��+a2n-1��+��b2+b4+��+b2n��
=$\frac{2��{4}^{n}-1��}{4-1}$-14n+$\frac{n��n-1��}{2}����-4��$=$\frac{2}{3}��{4}^{n}$-$\frac{2}{3}$-2n2-12n��
n=1��2��3ʱ��S2n��0��n��4ʱ������S2n��0������С��������n0=4��ʹ�õ�n��n0ʱ������S2n��0������
����S1=2��S2=-12��S3=-12+23=-4��S4=-22��S5=-22+25=10��
S6=-12��S7=-12+27=116��
�ɢٿ�֪��ʹ�õ�n��4ʱ������S2n��0��������an=2n��0��
���n��8ʱ������Sn��0����Sn����������
�������������m��n��m��n����ʹ��Sm=Sn������
��ȡm=2��n=6ʱ��Sm=Sn=-12������
��n��8ʱ������Sn��0����Sn����������S8=90�����Sm=Sn�����ܳ�����
���Ͽɵã�ֻ��m=2��n=6ʱ��ʹ��Sm=Sn������
���� ���⿼���˵Ȳ�������ȱ����е�ͨ�ʽ�����ʽ�����ƹ�ϵ�������˷������۷�������������������������������⣮


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3x-4y+18=0 | B�� | 4x+3y-1=0 | C�� | 4x-3y+17=0 | D�� | 4x+3y+1=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij���̶����Ϻ�����������ع��̣����ڱ߳�Ϊ1ǧ���������ε���ABC����Χѡ��һ��D��D��ƽ��ABC�ڣ�������һ�����÷ɻ��ܵ�AD���ڵ�D���B��C������ӽǡ�BDC=60�㣬��ͼ��ʾ���ǡ�CBD=�ȣ������Ʀȣ�ʹ�÷ɻ��ܵ�AD���
ij���̶����Ϻ�����������ع��̣����ڱ߳�Ϊ1ǧ���������ε���ABC����Χѡ��һ��D��D��ƽ��ABC�ڣ�������һ�����÷ɻ��ܵ�AD���ڵ�D���B��C������ӽǡ�BDC=60�㣬��ͼ��ʾ���ǡ�CBD=�ȣ������Ʀȣ�ʹ�÷ɻ��ܵ�AD����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | i+2 | B�� | i-2 | C�� | $\sqrt{5}$ | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
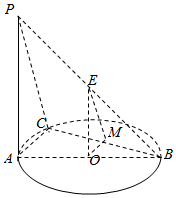 ��ͼ��ʾ��ABΪ��O��ֱ������C�ڡ�O�ϣ�PA��ƽ��ABC����EΪ�߶�PB���е㣬��MΪBC���е㣮
��ͼ��ʾ��ABΪ��O��ֱ������C�ڡ�O�ϣ�PA��ƽ��ABC����EΪ�߶�PB���е㣬��MΪBC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com