
【题目】已知偶函数![]() 在
在![]() 上单调递增,则
上单调递增,则
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:根据偶函数的定义,以及f(x)在(0,+∞)上单调递增,这样根据函数单调性定义以及幂函数、指数函数和对数函数的单调性即可判断每个选项的正误,从而选出正确选项.
详解:f(x)为偶函数,且在(0,+∞)上单调递增;
A.f(﹣3e)=f(3e),且2e<3e;
∴f(2e)<f(3e);
∴f(2e)<f(﹣3e),∴该选项错误;
B.f(﹣e3)=f(e3),且e2<e3;
∴f(e2)<f(e3);
∴f(e2)<f(﹣e3),∴该选项错误;
C.![]() ,
,![]() ;
;
∴![]() ;
;
∵f(x)是偶函数,且在(0,+∞)上单调递增;
∴f(x)在(﹣∞,0)上单调递减;
∴![]() ,∴该选项错误;
,∴该选项错误;
D.![]() ,
,![]() ;
;
∴![]() ;
;
∴![]() ,∴该选项正确.
,∴该选项正确.
故答案为:D


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin(2x+ ![]() ),若将它的图象向右平移
),若将它的图象向右平移 ![]() 个单位,得到函数g(x)的图象,则函数g(x)图象的一条对称轴的方程为( )
个单位,得到函数g(x)的图象,则函数g(x)图象的一条对称轴的方程为( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xea﹣x+bx,曲线y=f(x)在点(2,f(2))处的切线方程为y=(e﹣1)x+4,
(1)求a,b的值;
(2)求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2. 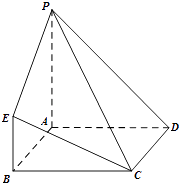
(1)求证:CE∥平面PAD;
(2)求PD与平面PCE所成角的正弦值;
(3)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE?如果存在,求 ![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的方程为(x﹣ ![]() )2+(y+1)2=9,以O为极点,x轴的非负半轴为极轴建立极坐标系.
)2+(y+1)2=9,以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线OP:θ= ![]() (p∈R)与圆C交于点M,N,求线段MN的长.
(p∈R)与圆C交于点M,N,求线段MN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( ) 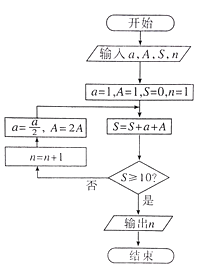
A.4
B.5
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆: ![]() (a>b>0),左右焦点分别是F1 , F2 , 焦距为2c,若直线
(a>b>0),左右焦点分别是F1 , F2 , 焦距为2c,若直线 ![]() 与椭圆交于M点,满足∠MF1F2=2∠MF2F1 , 则离心率是( )
与椭圆交于M点,满足∠MF1F2=2∠MF2F1 , 则离心率是( )
A.![]()
B.![]() -1
-1
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R.a,b∈R,若此函数同时满足:
①当a+b=0时,有f(a)+f(b)=0;
②当a+b>0时,有f(a)+f(b)>0,
则称函数f(x)为Ω函数.
在下列函数中:
①y=x+sinx;
②y=3x﹣( ![]() )x;
)x;
③y= 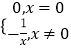
是Ω函数的为 . (填出所有符合要求的函数序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com