
分析 (1)讨论x的范围,去掉绝对值可得分段函数,再由一次函数的单调性可得最小值;
(2)由题意可得ax+x≥2,即有a≥$\frac{2}{x}$-1,运用单调性求得右边函数的最大值,可得a的范围.
解答 解:(1)f(x)=|x+2|+x-1,
即有f(x)=$\left\{\begin{array}{l}{2x+1,x≥-2}\\{-3,x<-2}\end{array}\right.$,
当x≥-2时,可得f(x)≥-3,
则f(x)的最小值为-3;
(2)对?x≥1,f(x)≥3成立,
即有|ax+2|+x-1≥3,
由a>0,x≥1,可得ax+x≥2,
即有a≥$\frac{2}{x}$-1,
由$\frac{2}{x}$-1≤2-1=1,
可得a≥1,即a的范围是[1,+∞).
点评 本题考查含绝对值函数的最值的求法,注意运用分段函数的单调性,考查不等式恒成立问题的解法,注意运用参数分离,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
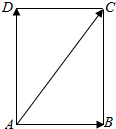 一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.
一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+$\frac{16}{x}$ | B. | x2+$\frac{16}{x}$ | C. | x+$\frac{32}{{x}^{2}}$ | D. | x+$\frac{36}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com