
分析 由点到直线的距离公式写出点(0,b)到直线3x-4y-a=0的距离,结合$\frac{1}{a}$+$\frac{1}{b}$=1(a>0,b>0)利用基本不等式求最值.
解答 解:∵a>0,b>0,且$\frac{1}{a}$+$\frac{1}{b}$=1,
∴点(0,b)到直线3x-4y-a=0的距离:
d=$\frac{|-4b-a|}{5}$=$\frac{1}{5}$(a+4b)($\frac{1}{a}$+$\frac{1}{b}$)=$\frac{1}{5}$(5+$\frac{a}{b}$+$\frac{4b}{a}$)≥$\frac{1}{5}$(5+4)=$\frac{9}{5}$
当且仅当,即a=3,b=$\frac{3}{2}$时上式等号成立.
∴点(0,b)到直线x3x-4y-a=0的距离的最小值为$\frac{9}{5}$.
故答案为:$\frac{9}{5}$.
点评 本题考查了点到直线的距离公式,考查了利用基本不等式求最值,是中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 6 | C. | 2$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
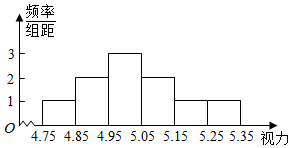 某市一高中经过层层上报,被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队,队员来自高中三个年级,人数为50人.视力对踢足球有一定的影响,因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间,将测量结果按如下方式分成6组:第一组[4.75,4.85),第二组[4.85,4.95),…,第6组[5.25,5.35],如图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中,全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布N(5.01,0.0064).
某市一高中经过层层上报,被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队,队员来自高中三个年级,人数为50人.视力对踢足球有一定的影响,因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间,将测量结果按如下方式分成6组:第一组[4.75,4.85),第二组[4.85,4.95),…,第6组[5.25,5.35],如图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中,全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布N(5.01,0.0064).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com