
分析 利用三角函数的诱导公式将函数进行化简,结合三角函数的图象和性质进行求解即可.
解答 解:$f(x)=sin(π-x)sin(\frac{π}{2}-x)+\sqrt{3}{cos^2}(π+x)-\frac{{\sqrt{3}}}{2}$
=sinxcosx+$\sqrt{3}$cos2x=$\frac{1}{2}$sin2x+$\sqrt{3}$×$\frac{1}{2}$(1+cos2x)
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x+$\frac{\sqrt{3}}{2}$
=sin(2x+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$,
则$f(\frac{π}{4})$=sin(2×$\frac{π}{4}$+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$=sin($\frac{π}{2}$+$\frac{π}{3}$)+$\frac{\sqrt{3}}{2}$=cos$\frac{π}{3}$+$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$,
∵-$\frac{π}{4}$≤x≤$\frac{π}{4}$,
∴-$\frac{π}{6}$≤2x+$\frac{π}{3}$≤$\frac{5π}{6}$,
∴当2x+$\frac{π}{3}$=-$\frac{π}{6}$时,f(x)取得最小值,
此时最小值为sin(-$\frac{π}{6}$)+$\frac{\sqrt{3}}{2}$=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$.
点评 本题主要考查三角函数值的求解以及三角函数的图象和性质,利用三角函数的诱导公式以及辅助角公式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
| 车次 | 芜湖发车 | 到达马鞍山东 | 耗时 |
| G7174 | 13:37 | 14:02 | 25分钟 |
| G7178 | 15:05 | 15:24 | 19分钟 |
| D5606 | 15:37 | 16:02 | 25分钟 |
| D5608 | 17:29 | 17:48 | 19分钟 |
| G7088 | 18:29 | 18:48 | 19分钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
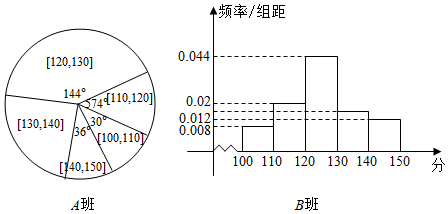
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:2:1 | B. | 3:1:2 | C. | 6:1:2 | D. | 6:2:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{5}-\frac{3}{5}i$ | B. | $\frac{1}{5}+\frac{3}{5}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [0,1) | C. | (一∞,1] | D. | (一∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com