
| A. | -2 | B. | 20 | C. | -160 | D. | 160 |
分析 根据微积分基本定理首先求出a的值,然后再根据二项式的通项公式求出k的值,问题得以解决.
解答 解:∵$a=\int_0^π{(cosx-sinx)dx}$|$\left.\begin{array}{l}{π}\\{0}\end{array}\right.$=-2,
∴${({x^2}+\frac{a}{x})^6}$=(x2-$\frac{2}{x}$)6
则${({x^2}+\frac{a}{x})^5}$展开式的通项公式为Tn+1=C${\;}_{6}^{k}$•(x2)6-k•($\frac{2}{x}$)k=(-2)k•C${\;}_{6}^{k}$•x12-3k,
令12-3k=3,
解得,k=3,
故二项式${({x^2}+\frac{a}{x})^6}$展开式中x3项的系数为-8×20=-160.
故选:C.
点评 本题主要考查了微积分基本定理和二项式的通项公式,培养了学生的计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | |||||
| 2x+$\frac{π}{6}$ | |||||
| sin(2x+$\frac{π}{6}$) | |||||
| f(x) |
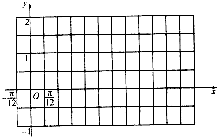
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+y+5=0 | B. | 2x-y-3=0 | C. | 3x-y-7=0 | D. | 3x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{6}}{2}$) | B. | (1,$\frac{\sqrt{6}}{2}$) | C. | ($\frac{\sqrt{6}}{2}$,+∞) | D. | (1,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin|x| | B. | y=|sinx| | C. | $y=sin\frac{x}{2}$ | D. | $y=cos\frac{x}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 烹调 | 包装 | 利润 | |
| A | 1 | 3 | 40 |
| B | 2 | 2 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com