
| x | |||||
| 2x+$\frac{π}{6}$ | |||||
| sin(2x+$\frac{π}{6}$) | |||||
| f(x) |
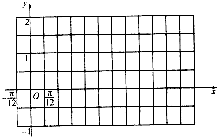
分析 (1)利用五点法,即将2x+$\frac{π}{6}$看成整体取正弦函数的五个关键点,通过列表、描点、连线画出函数图象,
(2)g(x)=f(x)+m=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$+m,x∈[-$\frac{π}{6}$,$\frac{π}{3}$],求此函数的最值可先将2x+$\frac{π}{6}$看成整体,求正弦函数的值域,最后利用函数g(x)=f(x)+m的最小值为2,解方程可得m的值,进而求出函数最大值.
解答 解:(1)列表如下:
| x | -$\frac{π}{12}$ | $\frac{2π}{12}$ | $\frac{5π}{12}$ | $\frac{8π}{12}$ | $\frac{11π}{12}$ |
| 2x+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| sin( 2x+$\frac{π}{6}$) | 0 | 1 | 0 | -1 | 0 |
| y | $\frac{1}{2}$ | $\frac{3}{2}$ | $\frac{1}{2}$ | -$\frac{1}{2}$ | $\frac{1}{2}$ |

点评 本题综合考察了三角变换公式的运用,三角函数的图象画法,三角函数图象变换,及复合三角函数值域的求法,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3+2$\sqrt{2}$ | D. | 3-2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,-2) | C. | (2,0) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 20 | C. | -160 | D. | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com