
分析 (1)利用赋值法,代入计算求f(1)和f(8)的值;
(2)由(1)把16f($\frac{1}{x-3}$)≥f(2x+1)转化为f($\frac{4}{x-3}$)≥f(2x+1),再由f(x)是定义在(0,+∞)上的增函数,可得$\left\{\begin{array}{l}{\frac{4}{x-3}>0}\\{2x+1>0}\\{\frac{4}{x-3}≥2x+1}\end{array}\right.$,求解不等式组得答案.
解答 解:(1)∵f(xy)=f(x)f(y),∴f(1×2)=f(1)f(2),
∵f(2)=4,∴f(1)=1,
f(4)=f(2)f(2)=16,f(8)=f(2)f(4)=64;
(2)由16f($\frac{1}{x-3}$)≥f(2x+1),得f(4)f($\frac{1}{x-3}$)≥f(2x+1),
即f($\frac{4}{x-3}$)≥f(2x+1),
∵f(x)是定义在(0,+∞)上的增函数,
∴$\left\{\begin{array}{l}{\frac{4}{x-3}>0}\\{2x+1>0}\\{\frac{4}{x-3}≥2x+1}\end{array}\right.$,即$\left\{\begin{array}{l}{x>3}\\{2{x}^{2}-5x-7≤0}\end{array}\right.$,
解得:3<x≤$\frac{7}{2}$.
∴不等式:16f($\frac{1}{x-3}$)≥f(2x+1)的解集为(3,$\frac{7}{2}$].
点评 本题考查抽象函数及其应用,考查了数学转化思想方法,是中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | $\overrightarrow{BE}$ | ||
| C. | $\overrightarrow{CF}$ | D. | 以上答案都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
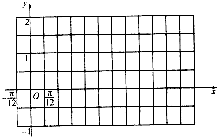
科目:高中数学 来源: 题型:解答题
| x | |||||
| 2x+$\frac{π}{6}$ | |||||
| sin(2x+$\frac{π}{6}$) | |||||
| f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+y+5=0 | B. | 2x-y-3=0 | C. | 3x-y-7=0 | D. | 3x-y-5=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin|x| | B. | y=|sinx| | C. | $y=sin\frac{x}{2}$ | D. | $y=cos\frac{x}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 4 | 1.5 | 4 | 1 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com