
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
分析 把已知向量等式$\overrightarrow{AB}$•$\overrightarrow{BC}$+$\overrightarrow{BC}$•$\overrightarrow{CA}$+$\overrightarrow{CA}$•$\overrightarrow{AB}$=-17变形,得到$\overrightarrow{AB}•\overrightarrow{BC}-|\overrightarrow{AC}{|}^{2}=-17$,代入|${\overrightarrow{AC}}$|=3得答案.
解答 解:由$\overrightarrow{AB}$•$\overrightarrow{BC}$+$\overrightarrow{BC}$•$\overrightarrow{CA}$+$\overrightarrow{CA}$•$\overrightarrow{AB}$=-17,得$\overrightarrow{AB}•\overrightarrow{BC}+\overrightarrow{CA}•(\overrightarrow{AB}+\overrightarrow{BC})=-17$,
即$\overrightarrow{AB}•\overrightarrow{BC}-|\overrightarrow{AC}{|}^{2}=-17$,
∵|${\overrightarrow{AC}}$|=3,∴$\overrightarrow{AB}•\overrightarrow{BC}=-17+{3}^{2}=-8$.
故选:D.
点评 本题考查平面向量的数量积运算,考查数学转化思想方法,是基础题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:解答题
| x | |||||
| 2x+$\frac{π}{6}$ | |||||
| sin(2x+$\frac{π}{6}$) | |||||
| f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 烹调 | 包装 | 利润 | |
| A | 1 | 3 | 40 |
| B | 2 | 2 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
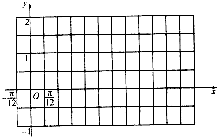
 已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,
已知函数f(x)的定义域[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,| x | -1 | 0 | 2 | 4 | 5 |
| f(x) | 1 | 4 | 1.5 | 4 | 1 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com