
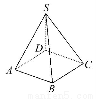
如图,将一个四棱锥的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种颜色可供使用,则不同的染色方法总数为( )
(A)60 (B)480
(C)420 (D)70
C
【解析】分两步,先将四棱锥一侧面三顶点染色,然后再分类考虑另外两顶点的染色数,用乘法原理可求解.
由题设,四棱锥S-ABCD的顶点S,A,B所染的颜色互不相同,它们共有5×4×3=60种染色方法.
当S,A,B染好时,不妨设所染颜色依次为1,2,3,若C染2,则D可染3或4或5,有3种染法;若C染4,则D可染3或5,有2种染法;若C染5,则D可染3或4,有2种染法,即当S,A,B染好时,C,D还有7种染法.
故不同的染色方法有60×7=420种.
【一题多解】以S,A,B,C,D的顺序分步染色.
第一步,S点染色,有5种方法;
第二步,A点染色,与S在同一条棱上,有4种方法;
第三步,B点染色,与S,A分别在同一条棱上有3种方法;
第四步,C点染色,也有3种方法,但考虑到D点与S,A,C相邻,需针对A与C是否同色进行分类,当A与C同色时,D点有3种染色方法,当A与C不同色时,因为C与S,B也不同色,所以C点有2种染色方法,D点也有2种染色方法.
由分步乘法计数原理,分类加法计数原理,得共有5×4×3×(1×3+2×2)=420种不同方法.
【方法技巧】涂色问题的两种解题方案
一是选择正确的涂色顺序,按步逐一涂色,这时用分步乘法计数原理逐一计数.
二是根据涂色时用颜色的多少,进行分类处理,这时用分类加法计数原理进行计数.
注意点:在分步涂色时,要尽量让相邻区域多的区域先涂,在分类涂色时要注意不相邻区域的颜色可相同也可不同,这是所用颜色多少的依据.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
已知函数f(x)=sinx+cosx,下列选项中正确的是( )
(A)f(x)在(-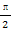 ,
,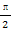 )上是递增的
)上是递增的
(B)f(x)的图象关于原点对称
(C)f(x)的最大值是2
(D)f(x)的最小正周期为2π
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:填空题
已知函数f(x)=3x+x-5的零点x0∈[a,b],且b-a=1,a,b∈N*,则a+b= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十第九章第一节练习卷(解析版) 题型:选择题
如果执行如图的程序框图,输入正整数N(N≥2)和实数a1,a2,…,aN,输出A,B,则( )
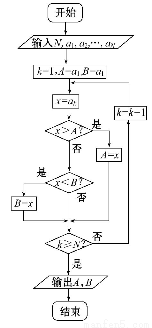
(A)A+B为a1,a2,…,aN的和
(B)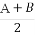 为a1,a2,…,aN的算术平均数
为a1,a2,…,aN的算术平均数
(C)A和B分别是a1,a2,…,aN中最大的数和最小的数
(D)A和B分别是a1,a2,…,aN中最小的数和最大的数
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:填空题
从集合{1,2,3,4,5,6,7,8,9,10}中选出五个数组成子集,使得这五个数中的任何两个数的和都不为11,这样的子集共有 个.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:选择题
如图所示,在连接正八边形的三个顶点而成的三角形中,与正八边形有公共边的三角形的个数为( )
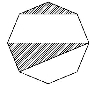
(A)8 (B)32 (C)40 (D)48
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十六第十章第三节练习卷(解析版) 题型:填空题
设(x-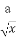 )6(a>0)的展开式中x3的系数为A,常数项为B.若B=4A,则a的值是 .
)6(a>0)的展开式中x3的系数为A,常数项为B.若B=4A,则a的值是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十八第十章第五节练习卷(解析版) 题型:填空题
一个质地均匀的正四面体(侧棱长与底面边长相等的正三棱锥)玩具的四个面上分别标有1,2,3,4这四个数字.若连续两次抛掷这个玩具,则两次向下的面上的数字之积为偶数的概率是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十二第九章第三节练习卷(解析版) 题型:选择题
某班有50名学生,该班某次数学测验的平均分为70分,标准差为s,后来发现成绩记录有误:甲生得了80分,却误记为50分;乙生得了70分,却误记为100分.更正后得标准差为s1,则s与s1之间的大小关系为( )
(A)s<s1 (B)s>s1
(C)s=s1 (D)无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com