
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为![]() 个,零件的实际出厂单价为
个,零件的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元? (工厂售出一个零件的利润=实际出厂单价-单件成本)
【答案】(1)当一次订购量为550个时,每个零件的实际出厂价恰好降为51元;(2)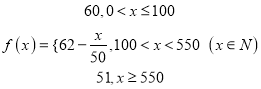 ;(3)当销售商一次订购500个零件时,该厂获得的利润为6000元.
;(3)当销售商一次订购500个零件时,该厂获得的利润为6000元.
【解析】试题分析:⑴根据题目要求列式运算即可得到答案;
⑵根据![]() 在不同范围时,关于
在不同范围时,关于![]() 的函数不同,为分段函数,即可求得答案;
的函数不同,为分段函数,即可求得答案;
⑶写出利润![]() 的表达式,在
的表达式,在![]() 的每一段上求最值,比较即可得到如何获得最大利润以及最大利润为多少;
的每一段上求最值,比较即可得到如何获得最大利润以及最大利润为多少;
解析:(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为xo个,则xo=100+![]() =550,
=550,
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元,
(2)当0<x≤100时,P=60,
当100<x<550时,P=60﹣0.02(x﹣100)=62﹣![]() ,
,
当x≥550时 P=51,
P=f(x)=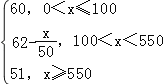 (x∈N)
(x∈N)
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,则
L=(P﹣40)x=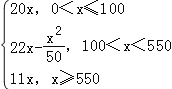 (x∈N)
(x∈N)
当x=500时 L=6000.当销售商一次订购500个零件时,该厂获得的利润为6000元.


科目:高中数学 来源: 题型:
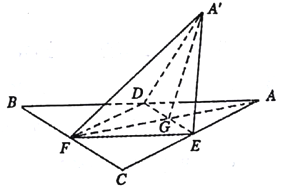
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,给出以下四个命题:①
旋转过程中的一个图形,给出以下四个命题:①![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③动点
;③动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上;④异面直线
上;④异面直线![]() 与
与![]() 不可能垂直. 其中正确命题的个数是( )
不可能垂直. 其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在线段PD上.
,PA=2,点M在线段PD上.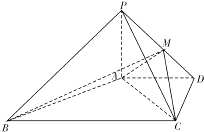
(1)求证:AB⊥PC.
(2)若二面角M﹣AC﹣D的大小为45°,求BM与平面PAC所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(Ⅰ)求角A的大小;
(Ⅱ)若△ABC的面积S=5 ![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】脱贫是政府关注民生的重要任务,了解居民的实际收入状况就显得尤为重要.现从某地区随机抽取![]() 个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第
个农户,考察每个农户的年收入与年积蓄的情况进行分析,设第![]() 个农户的年收入
个农户的年收入![]() (万元),年积蓄
(万元),年积蓄![]() (万元),经过数据处理得
(万元),经过数据处理得![]()
(Ⅰ)已知家庭的年结余![]() 对年收入
对年收入![]() 具有线性相关关系,求线性回归方程;
具有线性相关关系,求线性回归方程;
(Ⅱ)若该地区的农户年积蓄在![]() 万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
万以上,即称该农户已达小康生活,请预测农户达到小康生活的最低年收入应为多少万元?
附:在![]() 中,
中, 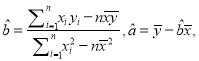 其中
其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称函数
称函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在第(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com