Question

6．三棱锥P-ABC中，△ABC为等边三角形，PA=PB=PC=2，PA⊥PB，三棱锥P-ABC的外接球的表面积为（　　）

• A． 48π
• B． 12π
• C． 4$\sqrt{3}$π
• D． 32$\sqrt{3}$π

Answer 1

分析 证明PA⊥PC，PB⊥PC，以PA、PB、PC为过同一顶点的三条棱，作长方体如图，则长方体的外接球同时也是三棱锥P-ABC外接球．算出长方体的对角线即为球直径，结合球的表面积公式，可算出三棱锥P-ABC外接球的表面积．

解答 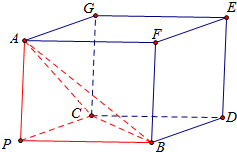解：∵三棱锥P-ABC中，△ABC为等边三角形，PA=PB=PC=2，
∴△PAB≌△PAC≌△PBC
∵PA⊥PB，
∴PA⊥PC，PB⊥PC
以PA、PB、PC为过同一顶点的三条棱，作长方体如图
则长方体的外接球同时也是三棱锥P-ABC外接球．
∵长方体的对角线长为$\sqrt{4+4+4}$=2$\sqrt{3}$，
∴球直径为2$\sqrt{3}$，半径R=$\sqrt{3}$，
因此，三棱锥P-ABC外接球的表面积是4πR²=4π×（$\sqrt{3}$）²=12π
故选：B．

点评 本题给出三棱锥的三条侧棱两两垂直，求它的外接球的表面积，着重考查了长方体对角线公式和球的表面积计算等知识，属于基础题．