
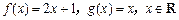 ,数列
,数列 ,
,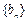 满足条件:
满足条件: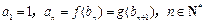 .
.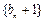 为等比数列;
为等比数列;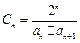 ,Tn是数列
,Tn是数列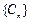 的前n项和,求使
的前n项和,求使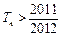 成立的最小的n值.
成立的最小的n值.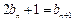 ,
,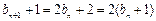 ········································································ 3分
········································································ 3分

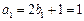

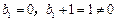 ················································································ 4分
················································································ 4分 数列{bn + 1}是以1为首项,2为公比的等比数列············································· 5分
数列{bn + 1}是以1为首项,2为公比的等比数列············································· 5分 ,∴
,∴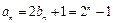 ·········································· 7分
·········································· 7分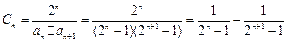 ················································ 9分
················································ 9分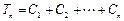
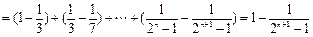 ············································ 10分
············································ 10分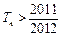 ,得
,得


科目:高中数学 来源:不详 题型:单选题
| A.3 | B.4 | C.6 | D.8 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
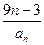 ,求数列{bn}的前n项和Tn。
,求数列{bn}的前n项和Tn。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
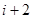 与第
与第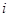 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中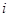 是自然数)。设白,黑蚂蚁都走完2011段后各停止在正方体的某个顶点处,这时黑,白两蚂蚁的距离是( )
是自然数)。设白,黑蚂蚁都走完2011段后各停止在正方体的某个顶点处,这时黑,白两蚂蚁的距离是( )| A.1 | B.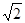 | C.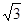 | D.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com