
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若![]() 只有一个极值点
只有一个极值点![]() .
.
(i)求实数![]() 的取值范围;
的取值范围;
(ii)证明:![]() .
.
【答案】(1) 最大值为-1. (2) (i)![]() (ii)证明见解析
(ii)证明见解析
【解析】
(1)当![]() 时,
时,![]() ,令
,令![]() ,利用导数求得函数的单调性,即可求得函数的最大值;
,利用导数求得函数的单调性,即可求得函数的最大值;
(2)由![]() ,得到
,得到![]() ,分
,分![]() 和
和![]() 讨论,求得函数的单调性与最值,结合函数的性质,即可得到答案.
讨论,求得函数的单调性与最值,结合函数的性质,即可得到答案.
(1)当![]() 时,
时,![]() ,
,![]() .
.
令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
∴![]() ,故
,故![]() 的最大值为-1.
的最大值为-1.
(2)![]() ,
,![]() .
.
①当![]() 时,
时,![]() 在
在![]() 恒成立,则
恒成立,则![]() 在
在![]() 单调递增.
单调递增.
而![]() ,当
,当![]() 时,
时,![]() ,
,
则![]() ,且
,且![]() ,∴
,∴![]() 使得
使得![]() .
.
∴当![]() 时,
时,![]() ,则
,则![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,则
,则![]() 单调递增,∴
单调递增,∴![]() 只有唯一极值点
只有唯一极值点![]() .
.
②当![]() 时,
时,![]()
当![]() 时,
时,![]() ,则
,则![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,则
,则![]() 单调递减,∴
单调递减,∴![]() .
.
(i)当![]() 即
即![]() 时,
时,![]() 在
在![]() 恒成立,则
恒成立,则![]() 在
在![]() 单调递减,无极值点,舍去.
单调递减,无极值点,舍去.
(ii)当![]() 即
即![]() 时,
时,![]() .
.
又![]() ,且
,且![]() ,∴
,∴![]() 使得
使得![]() .
.
由(1)知当![]() 时,
时,![]() ,则
,则![]()
∴![]()
则![]() ,且
,且![]() ,∴
,∴![]() 使得
使得![]() .
.
∴当![]() 时,
时,![]() ,则
,则![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,则
,则![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,则
,则![]() 单调递减.
单调递减.
∴![]() 有两个极值点
有两个极值点![]() ,
,![]() ,舍去.
,舍去.
综上,![]() 只有一个极值点时,
只有一个极值点时,![]()
∵![]() ,∴
,∴![]() ,
,![]()
∴![]() ,
,![]() .
.
令![]() ,∴
,∴![]() ,则
,则![]() 在
在![]() 单调递减
单调递减
∴当![]() 时,
时,![]() ,∴
,∴![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】汽车是碳排放量比较大的行业之一,欧盟规定,从2015年开始,将对![]() 排放量超过130g/km的
排放量超过130g/km的![]() 型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类
型新车进行惩罚(视为排放量超标),某检测单位对甲、乙两类![]() 型品牌抽取5辆进行
型品牌抽取5辆进行![]() 排放量检测,记录如下(单位:g/km):
排放量检测,记录如下(单位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | y | 160 |
经测算发现,乙品牌车![]() 排放量的平均值为
排放量的平均值为![]() .
.
(Ⅰ)从被检测的5辆甲类品牌中任取2辆,则至少有一辆![]() 排放量超标的概率是多少?
排放量超标的概率是多少?
(Ⅱ)若乙类品牌的车比甲类品牌的![]() 的排放量的稳定性要好,求x的范围.
的排放量的稳定性要好,求x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是一个三棱锥,
是一个三棱锥,![]() 是圆的直径,
是圆的直径,![]() 是圆上的点,
是圆上的点,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
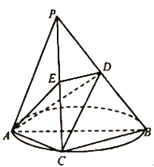
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点![]() 满足方程
满足方程![]() .
.
(1)求点M的轨迹C的方程;
(2)作曲线C关于![]() 轴对称的曲线,记为
轴对称的曲线,记为![]() ,在曲线C上任取一点
,在曲线C上任取一点![]() ,过点P作曲线C的切线l,若切线l与曲线
,过点P作曲线C的切线l,若切线l与曲线![]() 交于A,B两点,过点A,B分别作曲线
交于A,B两点,过点A,B分别作曲线![]() 的切线
的切线![]() ,证明
,证明![]() 的交点必在曲线C上.
的交点必在曲线C上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
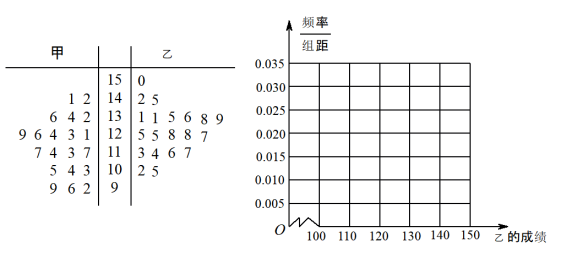
(1)根据茎叶图求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好?
(2)将同学乙的成绩的频率分布直方图补充完整;
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设选出的2个成绩中含甲的成绩的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标保持不变,纵坐标缩短为原来的
上的所有点的横坐标保持不变,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ;以坐标原点为极点,
;以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 交于不同的
交于不同的![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x+ay-1=0(a∈R)是圆C:x2+y2-4x-2y+1=0的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com