
已知A(x1,f(x1)),B(x2,f(x2))是函数f(x)=2sin(?x+?)(?>0, <?<0)图象上的任意两点,且角?的终边经过点P(l,-
<?<0)图象上的任意两点,且角?的终边经过点P(l,- ),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
),若|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 .
.
(1)求函数f(x)的解析式;(2)求函数f(x)的单调递增区间;(3)当x∈ 时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
时,不等式mf(x)+2m≥f(x)恒成立,求实数m的取值范围.
(1)f(x)=2sin(3x- );(2)[
);(2)[ +
+ ,
, +
+ ], k∈Z;(3)[
], k∈Z;(3)[ ,+?).
,+?).
【解析】
试题分析:(1)由角?的终边经过点P(l,-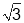 )及
)及 <?<0可求得?的值,又|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
<?<0可求得?的值,又|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 可最小正周期为
可最小正周期为 ,从而可求出?的值,即可求出其表达式;(2)由复合函数的知识可令3x-
,从而可求出?的值,即可求出其表达式;(2)由复合函数的知识可令3x- =u,只需令
=u,只需令 +2k?≤u≤
+2k?≤u≤ +2k?,解出x的范围即是函数的单调递增区间;(3)不等式mf(x)+2m≥f(x)恒成立要求m的范围,只需用分离变量的作法,等价于
+2k?,解出x的范围即是函数的单调递增区间;(3)不等式mf(x)+2m≥f(x)恒成立要求m的范围,只需用分离变量的作法,等价于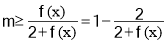 ,而x∈
,而x∈ ,可求出f(x)的范围,从而可求出
,可求出f(x)的范围,从而可求出 的最大值,则m恒大于或等于其最大值.
的最大值,则m恒大于或等于其最大值.
试题解析:(1)角?的终边经过点P(1,-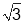 ),tan?=-
),tan?=-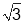 ,∵
,∵ <?<0,∴?=-
<?<0,∴?=- .由|f(x1)-f(x2)|=4时,|x1-x2|的最小值为
.由|f(x1)-f(x2)|=4时,|x1-x2|的最小值为 ,得T=
,得T= ,即
,即 =
= ,∴?=3,∴f(x)=2sin(3x-
,∴?=3,∴f(x)=2sin(3x- )
)
(2)令 +2k?≤3x-
+2k?≤3x- ≤
≤ +2k?,得
+2k?,得 +
+ ≤x≤
≤x≤ +
+ ,k∈Z
,k∈Z
∴函数f(x)的单调递增区间为[ +
+ ,
, +
+ ],k∈Z.
],k∈Z.
(3)当x∈ 时,-
时,-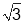 ≤f(x)≤1,所以2+f(x)>0,mf(x)+2m≥f(x)等价于
≤f(x)≤1,所以2+f(x)>0,mf(x)+2m≥f(x)等价于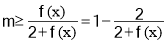 .由-
.由-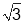 ≤f(x)≤1,得
≤f(x)≤1,得 的最大值为
的最大值为 ,所以实数m的取值范围是[
,所以实数m的取值范围是[ ,+?).
,+?).
考点:三角函数的定义,三角函数的周期公式,正弦函数的单调区间,恒成立问题,分离变量法,转化思想.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:高中数学 来源:2016届河南省周口市高一下学期期末考试数学试卷(解析版) 题型:选择题
在△ABC中,N是AC边上一点,且 ,P是BN上的一点,若
,P是BN上的一点,若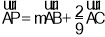 ,则实数m的值为( ).
,则实数m的值为( ).
A.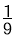 B.
B.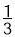 C.1 D.3
C.1 D.3
查看答案和解析>>
科目:高中数学 来源:2016届河南省周口市英文学校高一下学期期考试数学试卷(解析版) 题型:填空题
已知扇形的周长为8 cm,圆心角为2弧度,则该扇形的面积为_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com