①③④
分析:根据正弦函数的周期计算公式得①正确.
根据点(

,0)不是函数图象与x轴的交点,故函数图象不关于点(

,0)对称,故②不正确.
根据正弦函数的周期性,得函数y=f(x+t)为偶函数的一个充分必要条件,得③正确.
由于函数y=sinx的图象向左平移

个单位后,而得到y=sin(x+

),再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到 y=sin(2x+

),故④正确.
解答:对于①,由周期计算公式T=
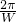
=

=π,得函数f(x)的最小正周期为π.正确;
对于②,因为当x=

时,函数f(x)=sin(2x+

)=1,故函数图象关于点(

,0)对称,故②不正确.
对于③函数y=f(x+t)=sin(2x+2t+

)为偶函数的一个充分必要条件是2t+

=

+kπ,k∈Z,
即t=

+kπ,k∈Z,特别地当k=0时,t=

,
故函数y=f(x+t)为偶函数的一个充分不必要条件是t=

;正确;
对于④,由于函数y=sinx的图象向左平移

个单位后,而得到y=sin(x+

),再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到 y=sin(2x+

),故④正确.
故答案为:①③④.
点评:本题考查正弦函数的对称性,以及y=Asin(ωx+∅)图象的变换,掌握y=Asin(ωx+∅)图象和性质是解题的关键.

 ),有如下结论:
),有如下结论: ,0)成中心对称;
,0)成中心对称; ;
; 个单位后,再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到y=f(x)的图象.
个单位后,再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到y=f(x)的图象. ,0)不是函数图象与x轴的交点,故函数图象不关于点(
,0)不是函数图象与x轴的交点,故函数图象不关于点( ,0)对称,故②不正确.
,0)对称,故②不正确. 个单位后,而得到y=sin(x+
个单位后,而得到y=sin(x+ ),再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到 y=sin(2x+
),再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到 y=sin(2x+ ),故④正确.
),故④正确.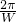 =
= =π,得函数f(x)的最小正周期为π.正确;
=π,得函数f(x)的最小正周期为π.正确; 时,函数f(x)=sin(2x+
时,函数f(x)=sin(2x+ )=1,故函数图象关于点(
)=1,故函数图象关于点( ,0)对称,故②不正确.
,0)对称,故②不正确. )为偶函数的一个充分必要条件是2t+
)为偶函数的一个充分必要条件是2t+ =
= +kπ,k∈Z,
+kπ,k∈Z, +kπ,k∈Z,特别地当k=0时,t=
+kπ,k∈Z,特别地当k=0时,t= ,
, ;正确;
;正确; 个单位后,而得到y=sin(x+
个单位后,而得到y=sin(x+ ),再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到 y=sin(2x+
),再把图象上各点的横坐标都缩短为原来的一半(纵坐标不变),便得到 y=sin(2x+ ),故④正确.
),故④正确.

 已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2,t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1、y轴所围成的封闭图形如阴影所示.
已知二次函数f(x)=ax2+bx+c,直线l1:y=-t2+8t(其中0≤t≤2,t为常数);l2:x=2.若直线l1、l2与函数f(x)的图象以及l1、y轴所围成的封闭图形如阴影所示. 已知二次函数f(x)=ax2+bx+c,直线l1:x=2,l2:y=-t2+8t(其中0≤t≤2.t为常数);若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
已知二次函数f(x)=ax2+bx+c,直线l1:x=2,l2:y=-t2+8t(其中0≤t≤2.t为常数);若直线l1、l2与函数f(x)的图象以及l1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.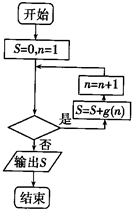 已知函数f(x)=ax3+
已知函数f(x)=ax3+