
分析 (1)利用幂函数的定义可知m=0或m=2,进而验证即得结论;
(2)通过(1)可知h(x)的图象是以x=b为对称轴、开口向下的抛物线(y轴及其右侧部分),分b≤0、0<b<2、b≥2三种情况讨论即可.
解答 解:(1)∵$f(x)={({m-1})^2}{x^{{m^2}-4m+3}}$为幂函数,
∴(m-1)2=1,解得m=0或m=2,
当m=0时,m2-4m+3=0-0+3=3,即f(x)=x3,满足题意;
当m=3时,m2-4m+3=9-12+3=0,即f(x)=1,不满足题意;
综上所述,实数m的值为0;
(2)由(1)可知$h(x)=-\root{3}{{{{[{f(x)}]}^2}}}+2bx+1-b$=-x2+2bx+1-b,x≥0,
∴h(x)的图象是以x=b为对称轴、开口向下的抛物线(y轴及其右侧部分),
当b≤0时,h(x)在[0,2]上单调递减,
此时h(x)max=h(0)=1-b=3,解得:b=-2,满足题意;
当0<b<2时,h(x)在[0,b)上单调递增、在(b,2]上单调递减,
此时h(x)max=h(b)=-b2+2b2+1-b=3,解得:b=2或b=-1,不满足题意;
当b≥2时,h(x)在[0,2]上单调递增,
此时h(x)max=h(2)=-4+4b+1-b=3,解得:b=2,满足题意;
综上所述,实数b的值为±2.
点评 本题考查利用导数研究函数的单调性,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {a|a>1} | B. | {a|a≥1} | C. | {a|a≤1} | D. | {a|0≤a≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
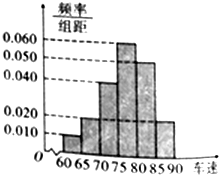 去年“十•一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费
去年“十•一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com