
 -
- )•
)• =________;若E是AB的中点,P是△ABC(包括边界)内任一点.则
=________;若E是AB的中点,P是△ABC(包括边界)内任一点.则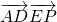 的取值范围是________.
的取值范围是________. =
= ,故
,故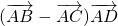 =
=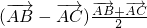 =
=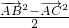 ,由此求得
,由此求得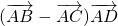 的值.以CA所在的直线为x轴,以CB所在的直线为y轴,建立平面直角坐标系,利用简单的线性规划求得t=
的值.以CA所在的直线为x轴,以CB所在的直线为y轴,建立平面直角坐标系,利用简单的线性规划求得t=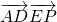 的取值范围.
的取值范围. =
= ,
, =
= +
+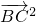 =16+4=20.
=16+4=20.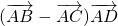 =
=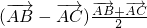 =
=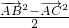 =
=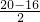 =2.
=2.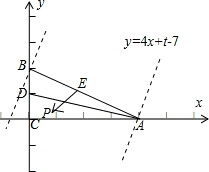
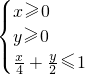 .
.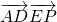 =(-4,1)•(x-2,y-1)=7-4x+y,即 y=4x+t-7.
=(-4,1)•(x-2,y-1)=7-4x+y,即 y=4x+t-7.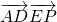 的取值范围是[-9,9],
的取值范围是[-9,9],

科目:高中数学 来源: 题型:
| AB |
| AC |
| AD |
| AD |
| EP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (几何证明选讲选做题)
(几何证明选讲选做题)| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com