
���� ��1�������⣬��������=�ܳɱ�+�����֪����0��x��400��x��400���������÷ֶκ�����ʾ��
��2����0��x��400��x��400�ֱ����������ֵ��ȡֵ��Χ���Ӷ�ȷ�����������ֵ���Ӷ��õ��������
��� �⣺��1�������⣬
��0��x��400ʱ��
f��x��=400x-0.5x2-20000-100x
=300x-0.5x2-20000��
��x��400ʱ��f��x��=80000-100x-20000
=60000-100x��
��$f��x��=\left\{\begin{array}{l}-\frac{1}{2}{x^2}+300x-20000����0��x��400��\\-100x+60000����x��400��\end{array}\right.$
��2����0��x��400ʱ��f��x��=300x-0.5x2-20000��
��x=300ʱ��f��x��max=f��300��=25000��Ԫ��
��x��400ʱ��f��x��max��f��400��=20000��Ԫ��
��25000��20000���൱x=300ʱ���ó�������������������Ϊ25000Ԫ��
���� ���⿼���˷ֶκ�����ʵ�������е�Ӧ�ã������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�$\overrightarrow{BF}=2\overrightarrow{FC}$��$\overrightarrow{AM}=\overrightarrow{MF}=\overrightarrow{FN}$��
��ͼ���ڡ�ABC�У�$\overrightarrow{BF}=2\overrightarrow{FC}$��$\overrightarrow{AM}=\overrightarrow{MF}=\overrightarrow{FN}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��+�ޣ� | B�� | ��-�ޣ�-1�� | C�� | ��-1��1�� | D�� | ��-2��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
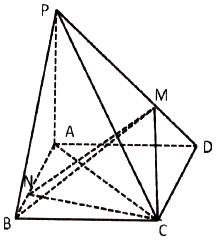 ��ͼ������P-ABCD�У�����ABCDΪƽ���ı��Σ�PA�͵���ABCD����PA=AB=AC=2��$BC=2\sqrt{2}$��
��ͼ������P-ABCD�У�����ABCDΪƽ���ı��Σ�PA�͵���ABCD����PA=AB=AC=2��$BC=2\sqrt{2}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com