
 随着手机和电脑的普及,人们收到垃圾短信也越来越多,小明在某社区进行垃圾短信问卷调查,从中随机抽取10人,在一个月内接到的垃圾短信条数统计的茎叶图如图所示:
随着手机和电脑的普及,人们收到垃圾短信也越来越多,小明在某社区进行垃圾短信问卷调查,从中随机抽取10人,在一个月内接到的垃圾短信条数统计的茎叶图如图所示:分析 (1)由已知求出样本平均数,由此能求出方差.
(2)由题意知,随机变量的可能取值为0,1,2,分别求出相应的概率,由此能求出随机变量X的分布列和E(X).
解答 解:(1)样本平均数为$\overline{x}$=$\frac{1}{10}$(4+8+15+16+17+18+20+22+30)=17,
方差为S2=$\frac{1}{10}$[(4-17)2+(8-17)2+…+(30-17)2]=46.8.
(2)由题意知,随机变量的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{8}^{2}}{{C}_{10}^{2}}$=$\frac{28}{45}$,P(X=1)=$\frac{{C}_{2}^{1}{C}_{8}^{1}}{{C}_{10}^{2}}$=$\frac{16}{45}$,P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{10}^{2}}$=$\frac{1}{45}$,
∴随机变量X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{28}{45}$ | $\frac{16}{45}$ | $\frac{1}{45}$ |
点评 本题考查样本的平均数及方差的求法,考查随机变量X的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∁R(M∩N) | B. | (∁RM)∩N | C. | (∁RM)∩(∁RN) | D. | M∩(∁RN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
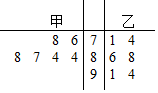 甲,乙两同学在高三上学期的6次联考测试中的物理成绩的茎叶图如图所示,则关于甲,乙两同学的成绩分析正确的是( )
甲,乙两同学在高三上学期的6次联考测试中的物理成绩的茎叶图如图所示,则关于甲,乙两同学的成绩分析正确的是( )| A. | 甲,乙两同学测试成绩的中位数相同 | |
| B. | 甲,乙两同学测试成绩的众数相同 | |
| C. | 甲,乙两同学测试成绩的平均数不相同 | |
| D. | 甲同学测试成绩的标准差比乙同学测试成绩的标准差大 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com