
| A. | ∁R(M∩N) | B. | (∁RM)∩N | C. | (∁RM)∩(∁RN) | D. | M∩(∁RN) |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{2},\frac{1}{2}}]$ | B. | $[{\frac{1}{2},+∞})$ | C. | $({-∞,\frac{1}{2}}]$ | D. | $({-∞,-\frac{1}{2}}]∪[{\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{4}$或$\frac{3π}{4}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 随着手机和电脑的普及,人们收到垃圾短信也越来越多,小明在某社区进行垃圾短信问卷调查,从中随机抽取10人,在一个月内接到的垃圾短信条数统计的茎叶图如图所示:
随着手机和电脑的普及,人们收到垃圾短信也越来越多,小明在某社区进行垃圾短信问卷调查,从中随机抽取10人,在一个月内接到的垃圾短信条数统计的茎叶图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
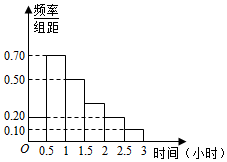 在2016年4月23日“世界读书日”到来之际,某单位对本单位全部200名员工平均每天的读书世界进行了调查,得到如图所示的频率分布直方图,根据该频率分步直方图,估计该单位每天平均读书时间在[1.5,2.5)之间的员工人数为50.
在2016年4月23日“世界读书日”到来之际,某单位对本单位全部200名员工平均每天的读书世界进行了调查,得到如图所示的频率分布直方图,根据该频率分步直方图,估计该单位每天平均读书时间在[1.5,2.5)之间的员工人数为50.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com