
分析 联立方程组消元,令方程无解或只有一解得出k的范围.
解答 解:把y=kx+1代入y2=2x得k2x2+(2k-2)x+1=0,
(1)若k=0,则-2x+1=0,方程只有一解,故直线y=kx+1与抛物线y2=2x只有一个公共点,符合题意.
(2)若k≠0,△=(2k-2)2-4k2=4-8k.
∵直线y=kx+1与抛物线y2=2x至多有一个公共点,
∴△=4-8k≤0,解得k$≥\frac{1}{2}$.
∴k$≥\frac{1}{2}$或k=0.
故答案为:{0}∪[$\frac{1}{2}$,+∞).
点评 本题考查了函数交点个数与方程解得个数的关系,二次方程根的个数判断,属于基础题.


科目:高中数学 来源: 题型:解答题
 在“2016”的logo设计中,有这样一个图案
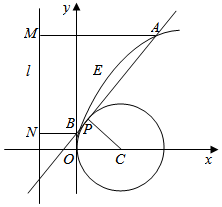
在“2016”的logo设计中,有这样一个图案 ,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.
,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∁R(M∩N) | B. | (∁RM)∩N | C. | (∁RM)∩(∁RN) | D. | M∩(∁RN) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
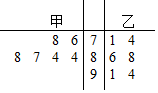 甲,乙两同学在高三上学期的6次联考测试中的物理成绩的茎叶图如图所示,则关于甲,乙两同学的成绩分析正确的是( )
甲,乙两同学在高三上学期的6次联考测试中的物理成绩的茎叶图如图所示,则关于甲,乙两同学的成绩分析正确的是( )| A. | 甲,乙两同学测试成绩的中位数相同 | |
| B. | 甲,乙两同学测试成绩的众数相同 | |
| C. | 甲,乙两同学测试成绩的平均数不相同 | |
| D. | 甲同学测试成绩的标准差比乙同学测试成绩的标准差大 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com