
| A. | $[{-\frac{1}{2},\frac{1}{2}}]$ | B. | $[{\frac{1}{2},+∞})$ | C. | $({-∞,\frac{1}{2}}]$ | D. | $({-∞,-\frac{1}{2}}]∪[{\frac{1}{2},+∞})$ |
分析 构造辅助函数$g(x)=f(x)-\frac{1}{3}{x^3}$,由f(x)是奇函数,g(-x)+g(x)=0,可知g(x)是奇函数,求导判断g(x)的单调性,$f(1-m)-f(m)≥\frac{1}{3}[{{{(1-m)}^3}-{m^3}}]$,即g(1-m)≥g(m),解得m的取值范围.
解答 解:令$g(x)=f(x)-\frac{1}{3}{x^3}$,
∵$g(-x)+g(x)=f(-x)-\frac{1}{3}{(-x)^3}+f(x)-\frac{1}{3}{x^3}=0$,
∴函数g(x)为奇函数,
∵x∈(0,+∞)时,
g′(x)=f′(x)-x2<0,
函数g(x)在x∈(0,+∞)为减函数,
又由题可知,f(0)=0,g(0)=0,
所以函数g(x)在R上为减函数,
$f(1-m)-f(m)≥\frac{1}{3}[{{{(1-m)}^3}-{m^3}}]$,即g(1-m)≥g(m),
∴1-m≤m,
∴$m≥\frac{1}{2}$.
故选B.
点评 本题主要考查判断函数的奇偶性、利用导数法求函数的单调性,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
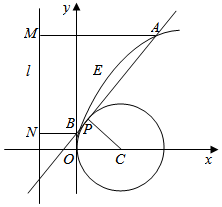 在“2016”的logo设计中,有这样一个图案
在“2016”的logo设计中,有这样一个图案 ,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.
,其由线段l、抛物线弧E及圆C三部分组成,对其进行代数化的分析,如图建系,发现:圆C方程为(x-4)2+y2=16,抛物线弧E:y2=2px(y≥0,0≤x≤8),若圆心C恰为抛物线y2=2px的焦点,线段l所在的直线恰为抛物线y2=2px的准线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
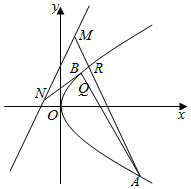 已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.
已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∁R(M∩N) | B. | (∁RM)∩N | C. | (∁RM)∩(∁RN) | D. | M∩(∁RN) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com