
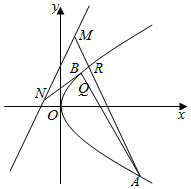
 已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.
已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.分析 (1)由点R(1,2)在抛物线C:y2=2px(p>0)上,求出p=2,由此能求出抛物线C的方程.
(2)设A(x1,y1),B(x2y2),设直线AB的方程为x=m(y-1)+1,m≠0,设直线AR的方程为y=k1(x-1)+2,由已知条件推导出xM=-$\frac{2}{{y}_{1}}$,xN=-$\frac{2}{{y}_{2}}$,由此求出|MN|=2$\sqrt{5}$$\frac{\sqrt{{m}^{2}-m+1}}{|m-1|}$,再用换元法能求出|MN|的最小值及此时直线AB的方程.
解答 解:(1)∵点R(1,2)在抛物线C:y2=2px(p>0)上,
∴4=2p,解得p=2,
∴抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2y2),直线AB的方程为x=m(y-1)+1,m≠0,
由$\left\{\begin{array}{l}{x=m(y-1)+1}\\{{y}^{2}=4x}\end{array}\right.$,消去x,并整理,得:y2-4my+4(m-1)=0,
∴y1+y2=4m,y1•y2=4(m-1),
设直线AR的方程为y=k1(x-1)+2,
由$\left\{\begin{array}{l}{y={k}_{1}(x-1)+2}\\{y=2x+2}\end{array}\right.$,解得点M的横坐标xM=$\frac{{k}_{1}}{{k}_{1}-2}$,
又k1=$\frac{{y}_{1}-2}{{x}_{1}-1}$=$\frac{4}{{y}_{1}+2}$,
∴xM=$\frac{{k}_{1}}{{k}_{1}-2}$=-$\frac{2}{{y}_{1}}$,
同理点N的横坐标xN=-$\frac{2}{{y}_{2}}$,
|y2-y1|=$\sqrt{({y}_{2}-{y}_{1})^{2}-4{y}_{1}{y}_{2}}$=4$\sqrt{{m}^{2}-m+1}$,
∴|MN|=|xM-xN|=$\sqrt{5}$|-$\frac{2}{{y}_{1}}$+$\frac{2}{{y}_{2}}$|=2$\sqrt{5}$|$\frac{{y}_{2}-{y}_{1}}{{y}_{2}{y}_{1}}$|,
=8$\sqrt{5}$$\frac{\sqrt{{m}^{2}-m+1}}{4|m-1|}$=2$\sqrt{5}$$\frac{\sqrt{{m}^{2}-m+1}}{|m-1|}$,
令m-1=t,t≠0,则m=t=1,
∴|MN|=2$\sqrt{5}$$\sqrt{(\frac{1}{t}+\frac{1}{2})^{2}+\frac{3}{4}}$≥$\sqrt{15}$,
即当t=-2,m=-1时,|MN|取最小值为$\sqrt{15}$,
此时直线AB的方程为x+y-2=0
点评 本题考查抛物线方程的求法,考查线段的最小值的求法,考查直线方程的求法,解题时要认真审题,注意换元法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
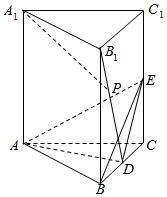 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,点D,E分别为BC,CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,点D,E分别为BC,CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | (0,-3) | C. | (0,3) | D. | (0,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{2},\frac{1}{2}}]$ | B. | $[{\frac{1}{2},+∞})$ | C. | $({-∞,\frac{1}{2}}]$ | D. | $({-∞,-\frac{1}{2}}]∪[{\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{4}$或$\frac{3π}{4}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
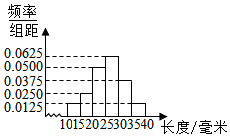 对一批产品的长度(单位:毫米)进行抽样检测,样本容量为200,如图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为50.
对一批产品的长度(单位:毫米)进行抽样检测,样本容量为200,如图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为50.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com