
分析 (Ⅰ)求得抛物线的焦点和准线方程,运用抛物线的定义解方程可得m=2p,求出P的坐标,可得抛物线的方程;
(Ⅱ)方法一、设直线AB的方程为y=kx+2,A(x1,y1),B(x2,y2),AB的中点Q(x0,y0),联立直线方程和抛物线方程,运用韦达定理和判别式大于0,中点坐标公式和弦长公式求得圆心和半径,可得以AB为直径的圆的方程,令x=0,可得M,N的坐标,再由向量的数量积的坐标表示,计算即可得证;
方法二:设A(x1,y1),B(x2,y2),M(0,m),N(0,n),求出向量MA,MB的坐标,由题意可得$\overrightarrow{MA}•\overrightarrow{MB}=0$,运用向量数量积的坐标表示,构造二次方程,运用韦达定理,以及联立直线方程和抛物线的方程,运用韦达定理,解方程即可得到定值.
解答 解:(Ⅰ)抛物线Γ:x2=2py的焦点为$F(0,\frac{p}{2})$,准线方程为$y=-\frac{p}{2}$.
∵P(4,m)到焦点F的距离为$\frac{5}{4}m$.
∴$|{PF}|=m+\frac{p}{2}=\frac{5}{4}m$,
∴m=2p,
∴P的坐标为(4,2p).
∴42=2p•2p.
∵p>0,
∴p=2,
∴抛物线Γ的方程为:x2=4y.
(Ⅱ)证法一、设直线AB的方程为y=kx+2,
A(x1,y1),B(x2,y2),AB的中点Q(x0,y0),
联立$\left\{\begin{array}{l}y=kx+2\\{x^2}=4y\end{array}\right.$,整理得:x2-4kx-8=0,
∴△=16k2+32>0,x1+x2=4k,
∴${x_0}=\frac{{{x_1}+{x_2}}}{2}=2k$,${y_0}=k{x_0}+2=2{k^2}+2$,
即Q(2k,2k2+2),
又$|{AB}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|$
=$\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$=$4\sqrt{(1+{k^2})(2+{k^2})}$,
∴以AB为直径的圆Q的方程为:(x-2k)2+(y-2k2-2)2=4(1+k2)(2+k2).
令x=0得,y2-(4k2+4)y-4=0.
设M(0,y3),N(0,y4),则y3y4=-4,
∴$\overrightarrow{OM}•\overrightarrow{ON}={y_3}{y_4}=-4$为定值.
证法二:设A(x1,y1),B(x2,y2),M(0,m),N(0,n),
则$\overrightarrow{MA}=({x_1},{y_1}-m),\overrightarrow{MB}=({x_2},{y_2}-m)$,
由已知可得$\overrightarrow{MA}•\overrightarrow{MB}=0$,
∴x1x2+(y1-m)(y2-m)=0,即m2-(y1+y2)m+(x1x2+y1y2)=0,
同理可得,n2-(y1+y2)n+(x1x2+y1y2)=0
∴m,n为方程x2-(y1+y2)x+(x1x2+y1y2)=0的两根,
∴$m•n={x_1}{x_2}+{y_1}{y_2}={x_1}{x_2}+{(\frac{{{x_1}{x_2}}}{4})^2}$,
联立$\left\{\begin{array}{l}y=kx+2\\{x^2}=4y\end{array}\right.$,整理得:x2-4kx-8=0,
∴△=16k2+32>0,x1•x2=-8,
∴m•n=-4,即$\overrightarrow{OM}•\overrightarrow{ON}=-4$为定值.
点评 本题主要考查直线、椭圆、轨迹等基础知识及直线与圆锥曲线的位置关系;考查运算求解能力、推理论证能力;考查化归与转化思想.


科目:高中数学 来源: 题型:选择题
| A. | -2p2 | B. | -p2 | C. | 0 | D. | 2p |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
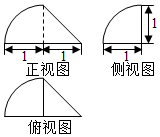
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
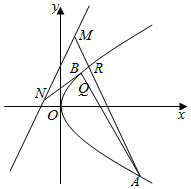 已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.
已知抛物线C的方程为y2=2px(p>0),点R(1,2)在抛物线C上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
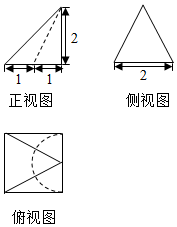 某空间几何体的三视图如图所示,则该几何体的体积为( )
某空间几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{7}{3}$ | B. | $\frac{8-π}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{7-π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com