练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．f（x）=（x-a）（x-b）（其中a＞b）的图象如图所示，则函数g（x）=loga（x-b）的图象大致是（　　）
    A．B．C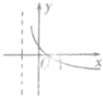．D．

    分析 根据二次函数的性质的得到a＞1，即-1＜b＜0，再根据对数函数的性质即可得到答案．

    解答 解：由f（x）=（x-a）（x-b）（其中a＞b）的图象可知，a＞1，即-1＜b＜0
    ∴g（x）=loga（x-b）图象单调递增，g（x）的图象是向左平移|b|个单位得到的，
    故选：B．

    点评 本题考查了函数图象的识别，关键是掌握函数的单调性和图象的平移，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．设α为锐角，若cos（α+$\frac{π}{6}$）=$\frac{3}{5}$，则cos（2α-$\frac{π}{6}$）=$\frac{24}{25}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

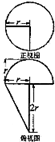    12．圆锥被一个平面截去一部分，剩余部分再被另一个平面截去一部分后，与半球（半径为r）组成一个几何体，则该几何体三视图中的正视图和俯视图如图所示，若r=1，则该几何体的体积为$\frac{5π}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．网格纸上小正方形的边长为1，如图画出的是某几何体的三视图，则该几何体的体积为（　　）
    A．44B．56C．68D．72

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知抛物线Γ：x2=2py（p＞0）上一点P（4，m）到焦点F的距离为$\frac{5}{4}m$．
    （Ⅰ）求Γ的方程；
    （Ⅱ）过点C（0，2）的直线交Γ于A，B两点，以AB为直径的圆交y轴于M，N两点，证明：$\overrightarrow{OM}•\overrightarrow{ON}$为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设变量x，y满足约束条件$\left\{\begin{array}{l}{y≤2x}\\{y≥\frac{1}{2}x}\\{x≤k}\end{array}\right.$，且目标函数z=2x+y的最大值为3，则k=$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．2016年高考报名体检中，某市共有40000名男生参加体检，体检其中一项为测量身高，统计调查数据显示所有男生的身高服从正态分布N（170，16），统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量，所得数据全部介于162cm和186cm之间，并将测量数据分成6组：第一组[162，166），第二组[166，170），…，第六组[182，186），然后按上述分组方式绘制得到如图所示的频率分布直方图．
    （1）试评估市一中高三年级参加体检的男生在全市高三年级参加体验的男生中的平均身高状况（同一组中的数据用该区间的中间值作代表）；
    （2）在这50名参加体检的男生身高在178cm以上（含178cm）的人中任意抽取3人，将该3人中身高排名（从高到低）在全市参加体检的高三男生身高前52名的人数记为X，求X的数学期望．
    参考数据：
    若X～N（μ，δ2），则P（μ-δ＜X≤μ+δ）=0.6826，P（μ-2δ＜X≤μ+2δ）=0.9544，P（μ-3δ＜X≤μ+3δ）=0.9974．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0）的图象与直线y=b（0＜b＜A）相交，其中一个交点P的横坐标为4，若与P相邻的两个交点的横坐标为2，8，则函数f（x）（　　）
    A．在[0，3]上是减函数B．在[-3，0]上是减函数
    C．在[0，π]上是减函数D．在[-π，0]上是减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，若AB=2，∠BAD=60°．则当四棱锥P-ABCD的体积等于2$\sqrt{3}$时，则PC=$\sqrt{21}$．

    查看答案和解析>>

    同步练习册答案