
 2016��߿���������У�ij�й���40000�������μ���죬�������һ��Ϊ�������ߣ�ͳ�Ƶ���������ʾ�������������߷�����̬�ֲ�N��170��16����ͳ����Ա����һ�и����IJμ����������������ȡ��50���������߲�������������ȫ������162cm��186cm֮�䣬�����������ݷֳ�6�飺��һ��[162��166�����ڶ���[166��170��������������[182��186����Ȼ���������鷽ʽ���Ƶõ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
2016��߿���������У�ij�й���40000�������μ���죬�������һ��Ϊ�������ߣ�ͳ�Ƶ���������ʾ�������������߷�����̬�ֲ�N��170��16����ͳ����Ա����һ�и����IJμ����������������ȡ��50���������߲�������������ȫ������162cm��186cm֮�䣬�����������ݷֳ�6�飺��һ��[162��166�����ڶ���[166��170��������������[182��186����Ȼ���������鷽ʽ���Ƶõ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ��1����Ƶ�ʷֲ�ֱ��ͼ�����У�����꼶�μ�����������ƽ�����ߣ��ɴ�����������
��2����Ƶ�ʷֲ�ֱ��ͼ֪������Ƶ��Ϊ0.12���Ӷ���50���μ�����������������ְ78cm���ϣ���178cm��������Ϊ6�ˣ������õ�ȫ�вμ�������������ǰ52����������182cm���ϣ��������X��ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ�ø�У�����꼶�μ�����������ƽ������Ϊ��
��164��$\frac{5}{100}$+168��$\frac{7}{100}$+172��$\frac{8}{100}$+176��$\frac{2}{100}$+180��$\frac{2}{100}$+184��$\frac{1}{100}$����4=170.72��cm����
����ȫ�е�ƽ��ֵ170cm��
��2����Ƶ�ʷֲ�ֱ��ͼ֪������Ƶ��Ϊ��0.02+0.01����4=0.12��
����Ϊ0.12��50=6��
����50���μ�����������������ְ78cm���ϣ���178cm��������Ϊ6�ˣ�
��P��170-3��4��X��170+3��4��=0.9974��
��P��X��182��=$\frac{1-0.9974}{2}$=0.0013��
0.0013��4000=52��
��ȫ�вμ�������������ǰ52����������182cm���ϣ�
��50���У�182cm���ϵ���0.01��4��5=2�ˣ�
���������X��ȡֵΪ0��1��2��
��P��X=0��=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$��
P��X=1��=$\frac{{C}_{2}^{1}{C}_{4}^{2}}{{C}_{6}^{3}}$=$\frac{3}{5}$��
P��X=2��=$\frac{{C}_{2}^{2}{C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{1}{5}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ����������ʵ������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��Сֵ10 | B�� | ��Сֵ100 | C�� | ���ֵ10 | D�� | ���ֵ100 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 f��x��=��x-a����x-b��������a��b����ͼ����ͼ��ʾ������g��x��=loga��x-b����ͼ������ǣ�������
f��x��=��x-a����x-b��������a��b����ͼ����ͼ��ʾ������g��x��=loga��x-b����ͼ������ǣ�������| A�� |  | B�� |  | C�� | 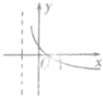 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��3} | B�� | {x|2��x��3} | C�� | N | D�� | R |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
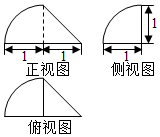
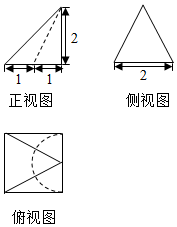 ij�ռ伸���������ͼ��ͼ��ʾ����ü���������Ϊ��������
ij�ռ伸���������ͼ��ͼ��ʾ����ü���������Ϊ��������| A�� | $\frac{7}{3}$ | B�� | $\frac{8-��}{3}$ | C�� | $\frac{8}{3}$ | D�� | $\frac{7-��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 672 | B�� | 673 | C�� | 1342 | D�� | 1344 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com