
分析 由cos(2α-$\frac{π}{6}$)=cos[(α+$\frac{π}{6}$)+(α-$\frac{π}{3}$)],分别根据诱导公式和同角的三角函数的关系即可求出答案.
解答 解:∵α为锐角,
∴α+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{2π}{3}$),α-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{π}{6}$)
∵cos(α+$\frac{π}{6}$)=$\frac{3}{5}$,
∴sin(α+$\frac{π}{6}$)=$\frac{4}{5}$,
∴cos(α+$\frac{π}{6}$)=sin[$\frac{π}{2}$-(α+$\frac{π}{6}$)]=sin($\frac{π}{3}$-α)=$\frac{3}{5}$,
∴sin(α-$\frac{π}{3}$)=-$\frac{3}{5}$,
∴cos(α-$\frac{π}{3}$)=$\frac{4}{5}$,
∴cos(2α-$\frac{π}{6}$)=cos[(α+$\frac{π}{6}$)+(α-$\frac{π}{3}$)]=cos(α+$\frac{π}{6}$)cos(α-$\frac{π}{3}$)-sin(α+$\frac{π}{6}$)sin(α-$\frac{π}{3}$)=$\frac{3}{5}$×$\frac{4}{5}$-$\frac{4}{5}$×(-$\frac{3}{5}$)=$\frac{24}{25}$,
故答案为:$\frac{24}{25}$
点评 本题着重考查了两角和与差的余弦公式,考查了三角函数中的恒等变换应用,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
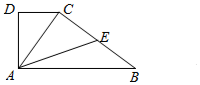 如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.
如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,AB=3,AD=$\sqrt{2}$,E为BC中点,若$\overrightarrow{AB}$•$\overrightarrow{AC}$=3,则$\overrightarrow{AE}$•$\overrightarrow{BC}$=-3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)岁年龄段中的参加者有8人.
某单位利用周末时间组织员工进行一次“健康之路,携手共筑”徒步走健身活动,有n人参加,现将所有参加人员按年龄情况分为[25,30),[30,35],[35,40),[40,45),[45,50),[50,55]六组,其频率分布直方图如图所示.已知[35,40)岁年龄段中的参加者有8人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com