
【题目】已知函数![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)当![]() 有两个极值点时,求a的取值范围,并证明
有两个极值点时,求a的取值范围,并证明![]() 的极大值大于2.
的极大值大于2.
【答案】(1)![]() 为(0,+∞)上的减函数.(2)见解析
为(0,+∞)上的减函数.(2)见解析
【解析】
(1)求出函数的导数,法1:结合二次函数的性质判断导函数的符号,求出函数的单调性即可;法2:令h(x)=(-x2+3x-3)ex-a,根据函数的单调性求出h(x)的最大值,判断即可;(2)令h(x)=(-x2+3x-3)ex-a,求出函数的导数,根据函数的单调性得到h(x)=0有两不等实数根x1,x2(x1<x2),求出a的范围,求出f(x)的极大值判断即可.
(1)由题知![]() .
.
方法1:由于![]() ,
,![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,从而
,从而![]() ,
,
于是![]() 为(0,+∞)上的减函数.
为(0,+∞)上的减函数.
方法2:令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数;当
为增函数;当![]() 时,
时,![]() ,
,![]() 为减函数.
为减函数.
则![]() .由于
.由于![]() ,所以
,所以![]() ,
,
于是![]() 为(0,+∞)上的减函数.
为(0,+∞)上的减函数.
(2)令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 为增函数;当
为增函数;当![]() 时,
时,![]() ,
, ![]() 为减函数.
为减函数.
当x趋近于![]() 时,
时, ![]() 趋近于
趋近于![]() ,
,
由于![]() 有两个极值点,所以
有两个极值点,所以![]() 有两不等实根,即
有两不等实根,即![]() 有两不等实数根
有两不等实数根![]() (
(![]() ).
).
则有![]() 解得
解得![]() .可知
.可知![]() ,
,
又![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
则函数![]() 在
在![]() 时取极小值,
时取极小值,![]() 在
在![]() 时取极大值.
时取极大值.
即![]() ,
,
而![]() ,即
,即![]() ,
,
所以极大值![]() .当
.当![]() 时,
时,![]() 恒成立,
恒成立,
故![]() 为
为![]() 上的减函数,所以
上的减函数,所以![]()


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,椭圆M:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,左右顶点分別为A,B,线段AB的长为4.P在椭圆M上且位于第一象限,过点A,B分别作l1⊥PA,l2⊥PB,直线l1,l2交于点C.
,左右顶点分別为A,B,线段AB的长为4.P在椭圆M上且位于第一象限,过点A,B分别作l1⊥PA,l2⊥PB,直线l1,l2交于点C.

(1)若点C的横坐标为﹣1,求P点的坐标;
(2)直线l1与椭圆M的另一交点为Q,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且二面角
的位置,且二面角![]() 为直二面角,连结
为直二面角,连结![]() .
.
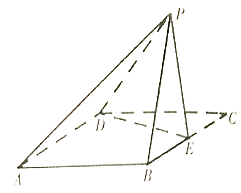
(1)记平面![]() 与平面
与平面![]() 相较于
相较于![]() ,在图中作出
,在图中作出![]() ,并说明画法;
,并说明画法;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为了响应疫情期间有序复工复产的号召,组织从疫区回来的甲、乙、丙、丁4名员工进行核酸检测,现采用抽签法决定检测顺序,在“员工甲不是第一个检测,员工乙不是最后一个检测”的条件下,员工丙第一个检测的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考改革后,国家只统一考试数学和语文,英语学科改为参加等级考试,每年考两次,分别放在每个学年的上、下学期,物理、化学、生物、地理、历史、政治这六科则以该省的省会考成绩为准.考生从中选择三科成绩,参加大学相关院系的录取.
(1)若英语等级考试成绩有一次为优,即可达到某211院校的录取要求.假设某个学生参加每次等级考试事件是独立的,且该生英语等级考试成绩为优的概率都是![]() ,求该生在高二上学期的英语等级考试成绩才为优的概率;
,求该生在高二上学期的英语等级考试成绩才为优的概率;
(2)据预测,要想报考该211院校的相关院系,省会考的成绩至少在90分以上,才有可能被该校录取.假设该生在省会考六科的成绩,考到90分以上概率都是![]() ,设该生在省会考时考到90分以上的科目数为
,设该生在省会考时考到90分以上的科目数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
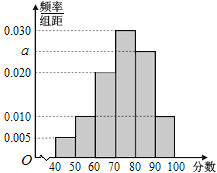
(1)求![]() 的值;
的值;
(2)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(3)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com