
在四棱锥 中,
中, //
// ,
, ,
, ,
, 平面
平面 ,
, .
.

(1)求证: 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)设点 为线段
为线段 上一点,且直线
上一点,且直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
(1)见解析(2) ,(3)
,(3)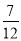
【解析】
试题分析:(1)建立如图所示坐标系,
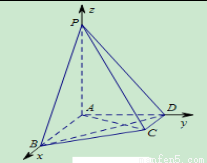
写出 坐标,可得
坐标,可得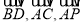 坐标,由
坐标,由 =
=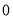 ,
,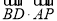 =
=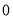 知
知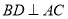 ,
,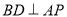 .所以
.所以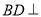 平面
平面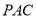 ;(2)由
;(2)由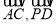 向量的夹角可知异成直线
向量的夹角可知异成直线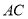 与
与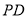 所成角;(3)
所成角;(3)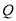 为线段
为线段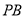 上一点,设
上一点,设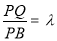 其中
其中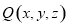 可得
可得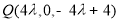 ,由直线
,由直线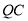 与平面
与平面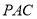 所成角的正弦值为
所成角的正弦值为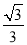 ,利用
,利用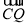 与平面
与平面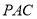 的法向量
的法向量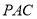 夹角,可得
夹角,可得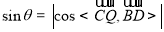 .其中
.其中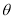 为直线
为直线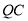 与平面
与平面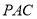 所成角.
所成角. .即
.即 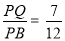 .
.
试题解析:(1)证明: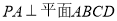 因为,
因为,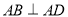 ,所以以
,所以以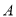 为坐标原点,
为坐标原点,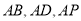 所在的直线分别为
所在的直线分别为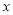 轴、
轴、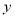 轴、
轴、 轴建立空间直角坐标系, 1分
轴建立空间直角坐标系, 1分
则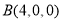 ,
,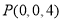 ,
,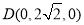 ,
,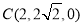 .
.
所以  ,
,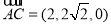 ,
,
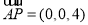 , 2分
, 2分
所以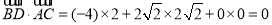 ,
,
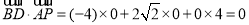 .
.
所以 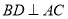 ,
,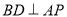 .
.
因为 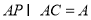 ,
,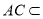 平面
平面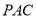 ,
,
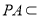 平面
平面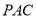 ,
,
所以 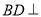 平面
平面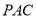 . 4分
. 4分
(2) 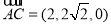 ,
,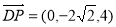 5分
5分
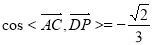
 异成直线
异成直线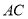 与
与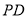 所成角的余弦值
所成角的余弦值 8分
8分
(3)【解析】
设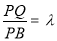 (其中
(其中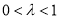 ),
),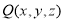 ,直线
,直线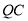 与平面
与平面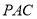 所成角为
所成角为 .
.
所以 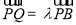 .所以
.所以 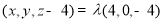 .
.
所以 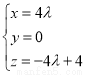 即
即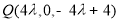 . 9分
. 9分
所以 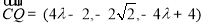 .
.
平面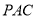 的一个法向量为
的一个法向量为 . 10分
. 10分
因为 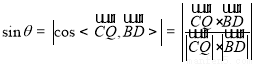 ,
,
所以 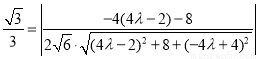 . 11分
. 11分
解得  .所以
.所以 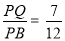 . 12分
. 12分
考点:本题主要考查空间向量的运算,线面之间的位置关系,线与线所成的角;考查空间想象能力,化归能力.


科目:高中数学 来源:2015届山东济宁鱼台二中高二3月质量检测理科数学试卷(解析版) 题型:选择题
函数 有( )
有( )
A.极大值 ,极小值
,极小值 B.极大值
B.极大值 ,极小值
,极小值
C.极大值 ,无极小值 D.极小值
,无极小值 D.极小值 ,无极大值
,无极大值
查看答案和解析>>
科目:高中数学 来源:2015届山东济宁任城一中高二下学期期中检测理科数学试卷(解析版) 题型:选择题
下列说法中正确的是( )
A.命题“若 ,则
,则 ”的否命题为假命题
”的否命题为假命题
B.命题“ 使得
使得
 ”的否定为“
”的否定为“ ,满足
,满足 ”
”
C.设 为实数,则“
为实数,则“ ”是“
”是“ ”的充要条件
”的充要条件
D.若“ ”为假命题,则
”为假命题,则 和
和 都是假命题
都是假命题
查看答案和解析>>
科目:高中数学 来源:2015届山东济宁任城一中高二下学期期中检测文科数学试卷(解析版) 题型:选择题
已知函数 的导函数为
的导函数为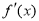 ,且满足关系式
,且满足关系式 ,则
,则 的值等于( )
的值等于( )
A. B.-1 C. 4 D.2
B.-1 C. 4 D.2
查看答案和解析>>
科目:高中数学 来源:2015届山东济宁任城一中高二下学期期中检测文科数学试卷(解析版) 题型:选择题
若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则实数a的取值范围是( )
A.(-∞,0]∪[1,+∞) B.(-1,0)
C.[-1,0] D.(-∞,-1)∪(0,+∞)
查看答案和解析>>
科目:高中数学 来源:2015届山东广饶一中高二上学期期末质量检测理科数学试卷B(解析版) 题型:填空题
给出下列命题:
(1)设 、
、 为两个定点,
为两个定点, 为非零常数,
为非零常数, ,则动点
,则动点 的轨迹为双曲线;
的轨迹为双曲线;
(2)若等比数列的前 项和
项和 ,则必有
,则必有 ;
;
(3)若 的最小值为2;
的最小值为2;
(4)双曲线 有相同的焦点;
有相同的焦点;
(5)平面内到定点(3,-1)的距离等于到定直线 的距离的点的轨迹是抛物线.
的距离的点的轨迹是抛物线.
其中正确命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届山东广饶一中高二上学期期末质量检测理科数学试卷B(解析版) 题型:选择题
设等比数列 的公比为
的公比为 ,前
,前 项和为
项和为 ,且
,且 .若
.若 ,则
,则 的取值范围是( )
的取值范围是( )
A.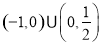 B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com