
| A. | 0<a≤5 | B. | a<5 | C. | 0<a<5 | D. | a≥5 |
分析 由题意可得必存在唯一的正实数a,满足f(x)+${log}_{\frac{1}{3}}x$=a,f(a)=4 ①,可得f(a)+${log}_{\frac{1}{3}}a$=a ②,由①②得a=${(\frac{1}{3})}^{a-4}$,解得a=3.由题意,|${log}_{\frac{1}{3}}x$|=x3-6x2+9x-4+a在区间(0,3]上有两解,数形结合可得a的范围.
解答 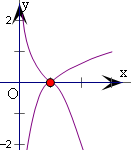 解:∵f(x)是定义域为(0,+∞)的单调函数,对任意的x∈(0,+∞),都有$f[{f(x)+{{log}_{\frac{1}{3}}}x}]=4$,
解:∵f(x)是定义域为(0,+∞)的单调函数,对任意的x∈(0,+∞),都有$f[{f(x)+{{log}_{\frac{1}{3}}}x}]=4$,
∴必存在唯一的正实数a,满足f(x)+${log}_{\frac{1}{3}}x$=a,f(a)=4 ①,∴f(a)+${log}_{\frac{1}{3}}a$=a ②,
由①②得:4+${log}_{\frac{1}{3}}a$=a,即 ${log}_{\frac{1}{3}}a$=a-4,∴a=${(\frac{1}{3})}^{a-4}$,解得a=3.
故f(x)+${log}_{\frac{1}{3}}x$=a=3,∴f(x)=3-${log}_{\frac{1}{3}}x$,
由方程|f(x)-3|=x3-6x2+9x-4+a在区间(0,3]上有两解,
即有|${log}_{\frac{1}{3}}x$|=x3-6x2+9x-4+a在区间(0,3]上有两解,
由g(x)=x3-6x2+9x-4+a,可得g′(x)=3x2-12x+9=3(x-1)(x-3),
当1<x<3时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)<0,g(x)递增.
g(x)在x=1处取得最大值a,g(0)=a-4,g(3)=a-4,
分别作出y=|${log}_{\frac{1}{3}}x$|,和y=x3-6x2+9x-4的图象,
可得两图象只有一个交点(1,0),将y=x3-6x2+9x-4的图象向上平移,
至经过点(3,1),有两个交点,由g(3)=1,即a-4=1,解得a=5,
当0<a≤5时,两图象有两个交点,即方程|f(x)-3|=x3-6x2+9x-4+a在区间(0,3]上有两解.
故选:A.
点评 本题考查对数的运算性质的综合运用,综合性强,难度大.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 若a2+b2≠0,则a,b都不为零 | B. | 若a2+b2≠0,则a,b不都为零 | ||
| C. | 若a,b都不为零,则a2+b2≠0 | D. | 若a,b不都为零,则a2+b2≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若 m∥α,n∥α,则 m∥n | B. | 若 m⊥α,n?α,则 m⊥n | ||
| C. | 若 m⊥α,m⊥n,则 n∥α | D. | 若 m∥α,m⊥n,则 n⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x≤0,$\frac{x-2}{x}$<0 | B. | ?x>0,$\frac{x-2}{x}$<0 | C. | ?x>0,0≤x<2 | D. | ?x>0,0<x<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | △y=f(x0+△x)-f(x0)叫函数值的改变量 | |
| B. | $\frac{△y}{△x}$=$\frac{f({x}_{0}+△x)-f({x}_{0})}{△x}$叫该函数在[x0,x0+△x]上的平均变化率 | |
| C. | f(x)在点x0处的导数记为y′ | |
| D. | f(x)在点x0处的导数记为f′(x0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
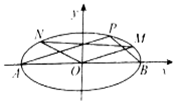 如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.
如图,点A(-2,0),B(2,0)分别为椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右顶点,P,M,N为椭圆C上非顶点的三点,直线AP,BP的斜率分别为k1,k2,且${k_1}{k_2}=-\frac{1}{4}$,AP∥OM,BP∥ON.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com