
分析 利用换元法,${(x+2)^2}+\frac{y^2}{4}=1$,可设x=cosθ-2,y=2sinθ,那么x2+y2=(cosθ-2)2+4sin2θ,利用三角函数的有界限求解即可.
解答 解:由题意:,${(x+2)^2}+\frac{y^2}{4}=1$,
设x=cosθ-2,y=2sinθ,
那么:x2+y2=(cosθ-2)2+4sin2θ=cos2θ-4cosθ+4+4sin2θ=cos2θ-4cosθ+8-4cos2θ=$-3(cosθ+\frac{2}{3})^{2}+\frac{4}{3}+8$,
当$cosθ=-\frac{2}{3}$时,x2+y2取值最大值为$\frac{28}{3}$.
当cosθ=1时,x2+y2取值最小值为1.
则x2+y2的取值范围是[1,$\frac{28}{3}$]
故答案为:[1,$\frac{28}{3}$]
点评 本题主要考查了最值的求法,利用了三角函数的有界限的性质,换元的思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | f(x)=x3 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=3x | D. | f(x)=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{10},1})$ | B. | $({\frac{1}{10},10})$ | C. | $({0,\frac{1}{10}})∪({1,+∞})$ | D. | (0,1)∪(10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③④ | C. | ②③④⑤ | D. | ③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
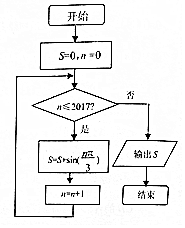 执行如图所示的程序框图,则输出S的值为( )
执行如图所示的程序框图,则输出S的值为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | 0 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com