
| A. | $({\frac{1}{10},1})$ | B. | $({\frac{1}{10},10})$ | C. | $({0,\frac{1}{10}})∪({1,+∞})$ | D. | (0,1)∪(10,+∞) |
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
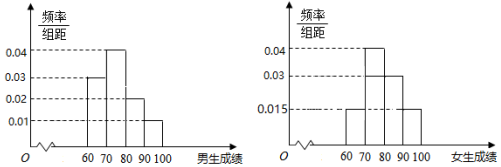
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 20 | 100 | 120 |
| 女 | 20 | 20 | 40 |
| 合计 | 40 | 120 | 160 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
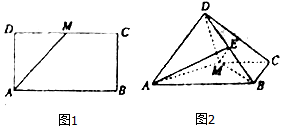 如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知长方形ABCD中,AB=2AD,M为DC的中点,将△ADM沿AM折起,使得平面ADM⊥平面ABCM.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{2},1})$ | B. | (-1,1)∪(1,2) | C. | (-∞,2) | D. | $[{-\frac{1}{2},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
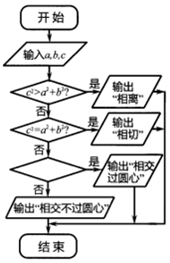 如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )
如图的程序框图,如果输入三个数a,b,c,(a2+b2≠0)要求判断直线ax+by+c=0与单位圆的位置关系,那么在空白的判断框中,应该填写下面四个选项中的( )| A. | c=0? | B. | b=0? | C. | a=0? | D. | ab=0? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com