
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
射击环数 | 频数 | 频率 |
7 | 10 | 0.1 |
8 | 10 | 0.1 |
9 | x | 0.45 |
10 | 35 | y |
合计 | 100 | 1 |
乙运动员
射击环数 | 频数 | 频率 |
7 | 8 | 0.1 |
8 | 12 | 0.15 |
9 | z |
|
10 |
| 0.35 |
合计 | 80 | 1 |
若将频率视为概率,回答下列问题:
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
(1) 0.35 (2) 0.992 (3) ξ的分布列是
ξ | 0 | 1 | 2 | 3 |
P | 0.01 | 0.11 | 0.4 | 0.48 |
2.35
【解析】由题意得x=100-(10+10+35)=45,
y=1-(0.1+0.1+0.45)=0.35.
因为乙运动员的射击环数为9时的频率为1-(0.1+0.15+0.35)=0.4,所以z=0.4×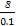 =32.
=32.
由上可得表中x处填45,y处填0.35,z处填32.
(1)设甲运动员射击1次击中10环为事件A,则P(A)=0.35,即甲运动员射击1次击中10环的概率为0.35.
(2)设甲运动员射击1次击中9环为事件A1,击中10环为事件A2,则甲运动员在1次射击中击中9环以上(含9环)的概率为P(A1∪A2)=P(A1)+P(A2)=0.45+0.35
=0.8,
故甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率P=1-[1-P(A1∪A2)]3=1-0.23=0.992.
(3)ξ的可能取值是0,1,2,3,则
P(ξ=0)=0.22×0.25=0.01,
P(ξ=1)=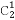 ×0.2×0.8×0.25+0.22×0.75=0.11,
×0.2×0.8×0.25+0.22×0.75=0.11,
P(ξ=2)=0.82×0.25+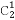 ×0.8×0.2×0.75=0.4,
×0.8×0.2×0.75=0.4,
P(ξ=3)=0.82×0.75=0.48.
所以ξ的分布列是
ξ | 0 | 1 | 2 | 3 |
P | 0.01 | 0.11 | 0.4 | 0.48 |
E(ξ)=0×0.01+1×0.11+2×0.4+3×0.48=2.35.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十一第五章第二节练习卷(解析版) 题型:解答题
等差数列{an}的首项为a1,公差d=-1,前n项和为Sn.
(1)若S5=-5,求a1的值.
(2)若Sn≤an对任意正整数n均成立,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷(解析版) 题型:解答题
已知△ABC,A(-1,0),B(3,0),C(2,1),对它先作关于x轴的反射变换,再将所得图形绕原点逆时针旋转90°.
(1)分别求两次变换所对应的矩阵M1,M2.
(2)求△ABC在两次连续的变换作用下所得到的△A'B'C'的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
抛掷两枚骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数X的期望是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:选择题
随机变量ξ的分布列如下:
ξ | -1 | 0 | 1 |
P | a | b | c |
其中a,b,c成等差数列,若E(ξ)= ,则D(ξ)的值是( )
,则D(ξ)的值是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:填空题
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
| 喜爱打篮球 | 不喜爱打篮球 | 总计 |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
总计 | 30 | 20 | 50 |
则在犯错误的概率不超过 的前提下认为喜爱打篮球与性别有关(请用百分数表示).
附:χ2=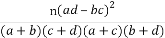
P(χ2≥x0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数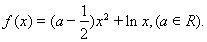
(Ⅰ)当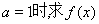 在区间
在区间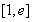 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间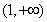 上,函数
上,函数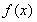 的图象恒在直线
的图象恒在直线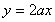 下方,求
下方,求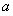 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com