
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
分析 由题设条件,结合向量法求出CD的长.
解答 解:如图,
∵在一个60°的二面角的棱上,有两个点A、B,AC、BD分别是在这个二面角的两个半平面内垂直于AB的线段,
AB=AC=1,BD=2,
∴$\overrightarrow{CA}•\overrightarrow{AB}=\overrightarrow{AB}•\overrightarrow{BD}=0$,<$\overrightarrow{CA},\overrightarrow{DB}$>=120°,
∴${\overrightarrow{CD}}^{2}=(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD})^{2}$=${\overrightarrow{CA}}^{2}+{\overrightarrow{AB}}^{2}+{\overrightarrow{BD}}^{2}+2\overrightarrow{CA}•\overrightarrow{AB}$$+2\overrightarrow{AB}•\overrightarrow{BD}+2\overrightarrow{CA}•\overrightarrow{BD}$
=1+1+4+2×1×2×cos120°=4.
∴|CD|=$|\overrightarrow{CD}|=2$.
故选:C.
点评 本题考查线段长的求法,解题时要注意空间思维能力的培养,注意向量法的合理运用,是中档题.


科目:高中数学 来源: 题型:解答题
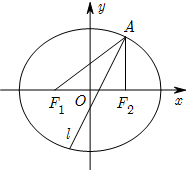 已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,焦距与长轴长的比为$\frac{1}{2}$.
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,焦距与长轴长的比为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2015,+∞) | D. | (-∞,0)∪(2015,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
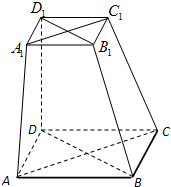 如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
如图,在六面体中ABCD-A1B1C1D1,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
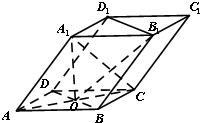 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com