
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2015,+∞) | D. | (-∞,0)∪(2015,+∞) |
分析 设g(x)=e-xf(x)-e-x,利用导数性质得y=g(x)在定义域上单调递增,从而得到g(x)>g(0),由此能求出f(x)>2015•ex+1(其中e为自然对数的底数)的解集.
解答 解:设g(x)=e-xf(x)-e-x,
则g′(x)=-e-xf(x)+e-xf′(x)+e-x=-e-x[f(x)-f′(x)-1],
∵f(x)-f′(x)<1,∴f(x)-f′(x)-1<0,
∴g′(x)>0,∴y=g(x)在定义域上单调递增,
∵f(x)>2015•ex+1,∴g(x)>2015,
∵g(0)=e-0f(0)-e-0=f(0)-1=2016-1=2015,
∴g(x)>g(0).∴x>0,
∴f(x)>2015•ex+1(其中e为自然对数的底数)的解集为(0,+∞).
故选:B.
点评 本题考查函数单调性与奇偶性的结合,结合已知条件构造函数,然后用导数判断函数的单调性是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | 8 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤4} | B. | {x|2<x≤3} | C. | {x|2≤x<3} | D. | {x|-1<x<4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
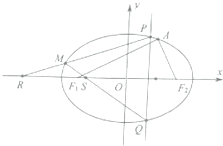 如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°
如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | [-1,+∞) | C. | (-∞,2] | D. | [-1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com