
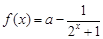 ,
,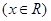 .
.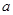 为何实数
为何实数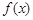 在
在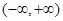 上为增函数;
上为增函数;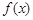 为奇函数,求
为奇函数,求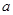 的值;
的值;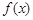 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.  ;(3)
;(3) .
. 的定义域为R, 任取
的定义域为R, 任取 ,------------1分
,------------1分 =
=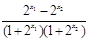 . -----------3分
. -----------3分 ,∴
,∴  .
. ,即
,即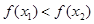 .
.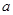 为何实数
为何实数 总为增函数.————————5分
总为增函数.————————5分 在
在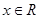 上为奇函数,
上为奇函数,  , ------------7分
, ------------7分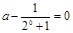 .解得
.解得  . —————————————10分
. —————————————10分 ,
,  为增函数,
为增函数,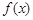 在区间
在区间 上的最小值为
上的最小值为 . ------------13分
. ------------13分 ,
,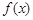 在区间
在区间 上的最小值为
上的最小值为 .———————————————15分
.———————————————15分

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com