
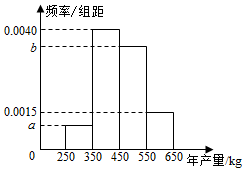
 某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.分析 (Ⅰ)由频率分布直方图的性质得到100(a+0.0015+b+0.004)=1,且300×100a+400×0.4+500×100b+600×0.15=455,由此能求出a,b.
(Ⅱ)由频率分布直方图能估计年销售额大于3600元小于6000元的概率.
解答 解:(Ⅰ)由频率分布直方图的性质得到:100(a+0.0015+b+0.004)=1,
得100(a+b)=0.45,(2分)
由300×100a+400×0.4+500×100b+600×0.15=455,
得300a+500b=2.05,(4分)
解得a=0.0010,b=0.0035.(6分)
(Ⅱ)由(Ⅰ)结合频率分布直方图知,
当年产量为300kg时,其年销售额为3600元,
当年产量为400kg时,其年销售额为4800元,
当年产量为500kg时,其年销售额为5000元,
当年产量为600kg时,其年销售额为6000元,(8分)
因为年产量为400kg的频率为0.4,即年销售额为4800元的频率为0.4,(9分)
而年产量为500kg的频率为0.35,即年销售额为5000元的频率为0.35,(10分)
故估计年销售额大于3600元小于6000元的概率为:0.35+0.4=0.75,(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\sqrt{10}$] | B. | [-$\sqrt{10}$,$\sqrt{10}$] | C. | [-3,$\sqrt{10}$] | D. | [$\sqrt{10}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | $\frac{9}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{9}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}+1$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k>1 | B. | k>-1 | C. | k<-$\frac{1}{2}$ | D. | k<-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com