
| A. | (-∞,-$\sqrt{10}$] | B. | [-$\sqrt{10}$,$\sqrt{10}$] | C. | [-3,$\sqrt{10}$] | D. | [$\sqrt{10}$,+∞) |
分析 根据对称函数的定义,结合h(x)≥g(x)恒成立,转化为点到直线的距离d≥1,利用点到直线的距离公式进行求解即可.
解答  解:∵x∈D,点(x,g(x)) 与点(x,h(x))都关于点(x,f(x))对称,
解:∵x∈D,点(x,g(x)) 与点(x,h(x))都关于点(x,f(x))对称,
∴$\frac{g(x)+h(x)}{2}$=f(x),
即2f(x)=g(x)+h(x)
∵h(x)≥g(x)恒成立,
∴2f(x)=g(x)+h(x)≥g(x)+g(x)=2g(x),
即f(x)≥g(x)恒成立,
作出g(x)和f(x)的图象,
若h(x)≥g(x)恒成立,
则h(x)在直线f(x)的上方,
即g(x)在直线f(x)的下方,
则直线f(x)的截距b>0,且原点到直线y=3x+b的距离d≥1,
即d=$\frac{|0-0+b|}{\sqrt{{3}^{2}+1}}$=$\frac{|b|}{\sqrt{10}}$≥1,即|b|≥$\sqrt{10}$,
则b≥$\sqrt{10}$或b≤-$\sqrt{10}$(舍),
即实数b的取值范围是[$\sqrt{10}$,+∞),
故选:D
点评 本题主要考查不等式恒成立问题,根据对称函数的定义转化为点到直线的距离关系,利用数形结合是解决本题的关键.综合性较强,有一定的难度.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 甲 | 89 | 91 | 90 | 88 | 92 |
| 乙 | 83 | 87 | 9● | 83 | 99 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
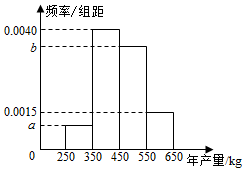 某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com