
| A. | 9 | B. | $\frac{9}{2}$ | C. | $\frac{9}{4}$ | D. | $\frac{9}{8}$ |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
| 甲 | 89 | 91 | 90 | 88 | 92 |
| 乙 | 83 | 87 | 9● | 83 | 99 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | $[\frac{1}{3},2]$ | C. | [0,4] | D. | $[\frac{1}{9},4]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
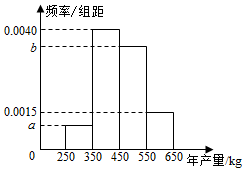 某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com