练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．从某班的一次数学测验试卷中任意抽出10份，其得分情况如下：81、98、43、75、60、55、78、84、90、70，则这次测验调查的样本方差为252.84．

    分析 根据平均数与方差的公式，利用计算器进行计算即可．

    解答 解：数据81、98、43、75、60、55、78、84、90、70的平均数是
    $\overline{x}$=$\frac{1}{10}$×（81+98+43+75+60+55+78+84+90+70）=73.4，
    则这次测验调查的样本方差为
    s2=$\frac{1}{10}$×[（81-73.4）2+（98-73.4）2+（43-73.4）2+（75-73.4）2
    +（60-73.4）2+（55-73.4）2+（78-73.4）2+（84-73.4）2+（90-73.4）2+（70-73.4）2]
    =252.84．
    故答案为：252.84．

    点评 本题考查了平均数与方差的计算问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=$\left\{\begin{array}{l}{2^x}，（x＜1）\\ f（x-1），（x≥1）\end{array}$，则f（log29）的值为（　　）
    A．9B．$\frac{9}{2}$C．$\frac{9}{4}$D．$\frac{9}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设a，b，c为三条不同的直线，α，β是两个不同的平面，则下列判断正确的是（　　）
    A．若a⊥b，b⊥c，则a⊥cB．若a∥α，b∥α，则a∥bC．若a∥α，b⊥α，则b∥αD．若a⊥α，α∥β，则a⊥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．在数列{an}中．已知a1=2，an+1=$\frac{2{a}_{n}}{{a}_{n}+1}$．
    （1）求证：{$\frac{1}{{a}_{n}}$-1}是等比数列
    （2）若对任意n∈N+，an＞m恒成立，求m的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若△ABC的面积为64，边AB与AC的等比中项为12，则sinA=（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\frac{3}{5}$C．$\frac{4}{5}$D．$\frac{8}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知实数x、y满足$\left\{\begin{array}{l}{x-y+2≥0}\\{x+2y+2≥0}\\{4x-y-10≤0}\end{array}\right.$，z=kx+y（k∈R）仅在（4，6）处取得最大值，则k的取值范围是（　　）
    A．k＞1B．k＞-1C．k＜-$\frac{1}{2}$D．k＜-4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

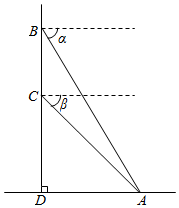    7．如图，山顶上有一座电视塔，在塔顶B处测得地面上一点A的俯角α=60°，在塔底C处测得点A的俯角β=45°，已知塔高60m，则山高为30（$\sqrt{3}$+1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=$\frac{m\sqrt{x}+lnx}{x}$（x＞0），m∈R，若函数f（x）的图象与x轴存在交点，求m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知三棱柱ABC-A1B1C1的侧棱垂直于底面，各顶点都在同一球面上，若该球的表面积为12π，AB=2，AC=1，∠BAC=60°，则此三棱柱的体积为$\sqrt{6}$．

    查看答案和解析>>

    同步练习册答案