
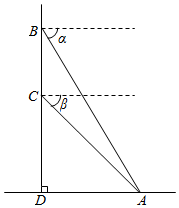
 如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).
如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1). 分析 根据题意构造直角三角形,本题涉及到两个直角三角形△DBA、△ADC,应利用其公共边AD构造等量关系,借助BC=DB-DC构造方程关系式,进而可求出答案.
解答 解:设山高CD=x(米),
∵∠CAD=∠β=45°,∠BAD=∠α=60°,∠ADB=90°,
∴AD=CD=x,BD=AD•tan60°=$\sqrt{3}$x.
∵BD-CD=BC=60,
∴$\sqrt{3}$x-x=60.
∴x=$\frac{60}{\sqrt{3}-1}$=30($\sqrt{3}$+1)(米).
故答案为:30($\sqrt{3}$+1).
点评 本题考查了学生借助俯角关系构造直角三角形,并结合图形利用三角函数解直角三角形.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ?n∈N*,anan+1≤an+2 | B. | ?n∈N*,an+an+2=2an+1 | ||
| C. | ?n∈N*,Sn<an+1 | D. | ?n∈N*,an+an+3=an+1+an+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com