
分析 由题意画出图形,可得$|\overrightarrow{AB}|=2|\overrightarrow{BD}|$,展开数量积$\overrightarrow{BH}•\overrightarrow{BC}$,结合向量在向量方向上的投影得到ac=12.运用余弦定理后再利用基本不等式求最值.
解答  解:如图,∵H是△ABC的垂心,且B=60°,
解:如图,∵H是△ABC的垂心,且B=60°,
∴$|\overrightarrow{AB}|=2|\overrightarrow{BD}|$
∴$\overrightarrow{BH}•\overrightarrow{BC}$=$|\overrightarrow{BH}||\overrightarrow{BC}|cos∠CBH$
=$|\overrightarrow{BD}||\overrightarrow{BC}|$=$\frac{1}{2}|\overrightarrow{AB}||\overrightarrow{BC}|=\frac{1}{2}ac=6$,
∴ac=12.
则b2=a2+c2-ac≥2ac-ac=ac=12,
∴bmin=2$\sqrt{3}$,
即AC的最小值为2$\sqrt{3}$.
故答案为:$2\sqrt{3}$.
点评 本题考查平面向量的数量积运算,关键是转化思想方法的运用,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
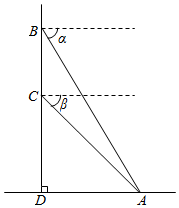 如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).
如图,山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角α=60°,在塔底C处测得点A的俯角β=45°,已知塔高60m,则山高为30($\sqrt{3}$+1).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6-π}{3π}$ | B. | 1 | C. | $\frac{π}{2}$ | D. | $\frac{4-π}{2π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com