
| A. | $\sqrt{2}+1$ | B. | $\sqrt{3}+1$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
分析 先根据双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{10}$=1的方程得出其左右焦点分别为F1(-2$\sqrt{3}$,0)、与F2(2$\sqrt{3}$,0),如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2的圆与直线l相切,求出圆心坐标,再利用相似三角形的知识得出$\frac{|P{F}_{1}|}{|P{F}_{2}|}$,最后利用相似比即可求出答案.
解答 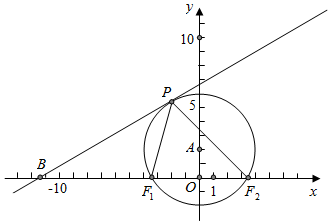 解:双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{10}$=1的左右焦点分别为
解:双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{10}$=1的左右焦点分别为
F1(-2$\sqrt{3}$,0)、F2(2$\sqrt{3}$,0).
如图,根据平面几何知识知,当∠F1PF2取最大值时,经过F1与F2的圆与直线l相切,
此时圆心在y轴上,坐标为A(0,2),
在直线l:x-$\sqrt{3}$y+8+2$\sqrt{3}$=0中,
令y=0得B的坐标:B(-8-2$\sqrt{3}$,0),
在三角形BPF1和三角形BF2P中,∠BPF1=∠BF2P,
∴△BPF1∽△BF2P,
∴$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\frac{|BP|}{|B{F}_{2}|}$=$\frac{\sqrt{A{B}^{2}-P{A}^{2}}}{BO+O{F}_{2}}$=$\frac{\sqrt{4+(8+2\sqrt{3})^{2}-(4+12)}}{8+2\sqrt{3}+2\sqrt{3}}$=$\sqrt{3}$-1.
故选:D.
点评 本小题主要考查直线与圆锥曲线的关系、直线与圆的位置关系、圆的切线等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 甲 | 89 | 91 | 90 | 88 | 92 |
| 乙 | 83 | 87 | 9● | 83 | 99 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
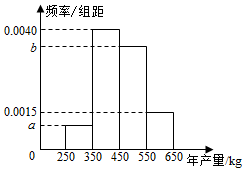 某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.
某人租用一块土地种植一种瓜类作物,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.已知当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg 时,单位售价为10元/kg.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com