
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,圆
,圆![]() .
.
(1)若过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)圆![]() 是以1为半径,圆心在圆
是以1为半径,圆心在圆![]() :
:![]() 上移动的动圆 ,若圆
上移动的动圆 ,若圆![]() 上任意一点
上任意一点![]() 分别作圆
分别作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若动圆![]() 同时平分圆
同时平分圆![]() 的周长、圆
的周长、圆![]() 的周长,则动圆
的周长,则动圆![]() 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
【答案】(1)![]() 或
或![]() (2)
(2)![]() (3)所求的定点坐标为
(3)所求的定点坐标为![]()
【解析】
试题分析:(Ⅰ)设直线l的方程为y=k(+1),根据直线l被圆C2截得的弦长为![]() ,利用勾股定理,求出k,即可求直线l的方程;(Ⅱ)动圆D是圆心在定圆
,利用勾股定理,求出k,即可求直线l的方程;(Ⅱ)动圆D是圆心在定圆![]() 上移动,半径为1的圆,由圆的几何性质得,|DC1|-r≤|PC1|≤|DC1|+r,即2≤|PC1|≤4,4≤|PC1|2≤16,利用向量的数量积公式,即可求
上移动,半径为1的圆,由圆的几何性质得,|DC1|-r≤|PC1|≤|DC1|+r,即2≤|PC1|≤4,4≤|PC1|2≤16,利用向量的数量积公式,即可求
![]() 的取值范围;(Ⅲ)确定动圆圆心C在定直线x+y-3=0上运动,求出动圆C的方程,即可得出结论.
的取值范围;(Ⅲ)确定动圆圆心C在定直线x+y-3=0上运动,求出动圆C的方程,即可得出结论.
试题解析:(1)设直线![]() 的方程为
的方程为![]() ,即
,即![]() . 因为直线
. 因为直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,而圆
,而圆![]() 的半径为1,所以圆心
的半径为1,所以圆心![]() 到
到![]() :
:![]() 的距离为
的距离为![]() .化简,得
.化简,得![]() ,解得
,解得![]() 或
或![]() .所以直线
.所以直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(2) 动圆D是圆心在定圆![]() 上移动,半径为1的圆
上移动,半径为1的圆

设![]() ,则在
,则在![]() 中,
中,![]() ,
,
有![]() ,则
,则![]()
由圆的几何性质得,![]() ,即
,即![]() ,
,![]()
则![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() . 故
. 故![]()
(3)设圆心C(x,y),由题意得CC1=CC2,
即![]() ,整理得x+y-3=0,即圆心C在定直线x+y-3=0上运动.
,整理得x+y-3=0,即圆心C在定直线x+y-3=0上运动.

设C(m,3-m),
则动圆的半径![]() ,
,
于是动圆C的方程为(x-m)2+(y-3+m)2=1+(m+1)2+(3-m)2,
整理得:x2+y2-6y-2-2m(x-y+1)=0.
由 ,
,
解得 或
或 ,
,
即所求的定点坐标为![]()


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段![]() 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_________(写出所有正确命题的编号)。
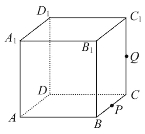
①当![]() 时,S为四边形
时,S为四边形
②当![]() 时,S为等腰梯形
时,S为等腰梯形
③当![]() 时,S与
时,S与![]() 的交点R满足
的交点R满足![]()
④当![]() 时,S为六边形
时,S为六边形
⑤当![]() 时,S的面积为
时,S的面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别为椭圆
分别为椭圆![]() :
:![]()
![]() 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)若椭圆![]() 上的点
上的点![]() 到
到![]() 、
、![]() 两点的距离之和等于6,写出椭圆
两点的距离之和等于6,写出椭圆![]() 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设点![]() 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段![]() 的中点M的轨迹方程.
的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为1,
的棱长为1,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于
交于![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
①四边形![]() 为平行四边形;
为平行四边形;
②若四边形![]() 面积
面积![]() ,
,![]() ,则
,则![]() 有最小值;
有最小值;
③若四棱锥![]() 的体积
的体积![]()
![]() ,
,![]() ,则
,则![]() 为常函数;
为常函数;
④若多面体![]() 的体积
的体积![]() ,
,![]() ,则
,则![]() 为单调函数.
为单调函数.
其中假命题为( )
A. ① ③ B. ② C. ③④ D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,圆
,圆![]() .
.
(1)若过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)圆![]() 是以1为半径,圆心在圆
是以1为半径,圆心在圆![]() :
:![]() 上移动的动圆 ,若圆
上移动的动圆 ,若圆![]() 上任意一点
上任意一点![]() 分别作圆
分别作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若动圆![]() 同时平分圆
同时平分圆![]() 的周长、圆
的周长、圆![]() 的周长,则动圆
的周长,则动圆![]() 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布如图所示.
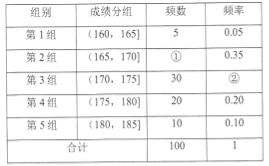
(1)请先求出频率分布表中①、②位置相应的数据,再画出频率分布直方图;
(2)该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受考官的面试,求第4组至少有一名学生被考官面试的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com