
已知函数f(x)的定义域为R,且满足f(x+2)=-f(x).
若f(x)为奇函数,且当0≤x≤1时 ,f(x)=
,f(x)=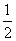 x,求使f(x)=-
x,求使f(x)=-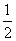 在[0,2 009]上的所有x的个数.
在[0,2 009]上的所有x的个数.
解 当0≤x≤1时,f(x)=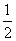 x,设-1≤x≤0,则0≤-x≤1,
x,设-1≤x≤0,则0≤-x≤1,
∴f(-x)=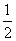 (-x)=-
(-x)=-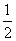 x.
x.
∵f(x)是奇函数,∴f(-x)=-f(x),
∴-f(x)=-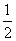 x,即f(x)=
x,即f(x)=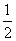 x.
x.
故f(x)=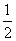 x (-1≤x≤1).
x (-1≤x≤1).
又设1<x<3,则-1<x-2<1,∴f(x-2)=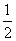 (x-2).
(x-2).
又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x) ,
,
∴-f(x)=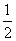 (x-2),
(x-2),
∴f(x)=-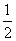 (x-2) (1<x<3).
(x-2) (1<x<3).
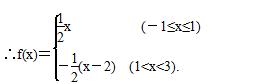 由f(x)=-
由f(x)=-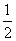 ,解得x=-1.
,解得x=-1.
又∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=-[-f(x)]=f(x),
∴f(x)是以4为周期的周期函数.
∴f(x)=-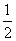 的所有x=4n-1 (n∈Z).
的所有x=4n-1 (n∈Z).
令0≤4n-1≤2 009,则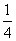 ≤n≤
≤n≤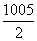 ,
,
又∵n∈Z,∴1≤n≤502 (n∈Z),
∴在[0,2 009]上共有502个x使f(x)=-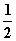 .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电 价调至0.55
价调至0.55
元~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿千瓦时)与(x-0.4)元成反比例.又当x=0.65时,y=0.8.
(1)求y与x之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益=用电量×(实际电价-成本价)]
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com