练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在三棱锥S—ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°。

    （1）求证：平面MAP⊥平面SAC。

    （2）求二面角M—AC—B的平面角的正切值；


    I）∵SC⊥平面ABC，SC⊥BC，又∵∠ACB=90°

    ∴AC⊥BC，AC∩SC=C，BC⊥平面SAC，

    又∵P，M是SC、SB的中点

    ∴PM∥BC，PM⊥面SAC，∴面MAP⊥面SAC，　　　　（５分）

       （II）∵AC⊥平面SBC，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知直线，圆.

    （1）若直线l与圆C相切，求实数m的值和直线l的方程；

    （2）若直线l与圆C相离，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过点作一直线与椭圆相交于A、B两点，若点恰好为弦的中点，则所在直线的方程为         ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正方体-中，与平面ABCD所成角的余弦值为(    )

    A．      B.    C.        D.

     


    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下面给出五个命题：

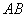    ① 已知平面//平面，是夹在间的线段，若//，则；

    ② 是异面直线，是异面直线，则一定是异面直线；

    ③ 三棱锥的四个面可以都是直角三角形。

    ④ 平面//平面，，//，则；

    ⑤ 三棱锥中若有两组对棱互相垂直，则第三组对棱也一定互相垂直；

      其中正确的命题编号是              （写出所有正确命题的编号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆上的一点到椭圆一个焦点的距离为，则到另一焦点距离为                                                                （   ）

    A   　　　　 B    　　　　 C   　　　　　　 D

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列命题错误的是   (    )

    A.命题“若”的逆否命题为“若 ”

    B. “”是“”的充分不必要条件

    C. 若为假命题，则均为假命题

    D. 对于命题则 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    顶点为原点，焦点为的抛物线方程是                               （    ）

       A.　     B. 　   C.       D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合M＝{1,2}，N＝{a2}，则“a＝1”是“N⊆M”的(　　)．

    A．充分不必要条件                                  B．必要不充分条件

    C．充分必要条件                                    D．既不充分又不必要条件

    查看答案和解析>>

    同步练习册答案