
已知g(x)=-x2-3,f(x)是二次函数,当x∈[-1,2]时,f(x)的最小值是1,且f(x)+g(x)是奇函数,求f(x)的表达式.
 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的底面直径与高的比为( )
A.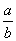 B.
B.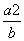 C.
C.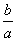 D.
D.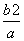
查看答案和解析>>
科目:高中数学 来源: 题型:
根据市场调查,某商品在最近40天内的价格P与时间t的关系用图1中的一条折线表示,销量Q与时间t的关系用图2中的线段表示(t∈N*).

(1)分别写出图1表示的价格与时间的函数关系P=f(t),图2表示的销售量与时间的函数关系Q=g(t);
(2)这种商品的销售额S(销售量与价格之积)的最大值及此时的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)=x2-2x-3,x∈[0, m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( )
m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( )
A.(0,1] B.[1,2]
C.[2,+∞) D.(0,2]
查看答案和解析>>
科目:高中数学 来源: 题型:
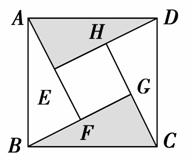
“赵爽弦图”是由于四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).现随机地在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是2和1,则针扎到阴影区域的概率是( )
A. B.
B.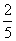 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
现有6道题,其中4道甲类题,2道乙类题,张同学从中任取2道题解答.试求:
(1)所取的2道题都是甲类题的概率;
(2)所取的2道题不是同一类题的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com