
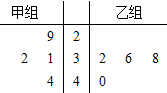
 ij�̳�Ϊ�������ص�ij���ز�������һ�δ���������ɳ��Ĵ���Ա�ֳɼס�������С��ֱ���������ͬ�ij��ؽ��д�����ÿ��С���4�ˣ����¾�Ҷͼ��¼��������С���Ա���������ز��ļ�����
ij�̳�Ϊ�������ص�ij���ز�������һ�δ���������ɳ��Ĵ���Ա�ֳɼס�������С��ֱ���������ͬ�ij��ؽ��д�����ÿ��С���4�ˣ����¾�Ҷͼ��¼��������С���Ա���������ز��ļ��������� �������������4����Ա�����ز�������ƽ�������Ӷ��õ�����4����Ա�������ļ����ȼ���ƽ���������3λͬѧ���ɴ����������������ѡ2λ����Ա�������Ǵ����ļ��������ڼ������������ƽ�����ĸ��ʣ�
������8������Ա��������������35���Ĺ���4�ˣ���X��ֵ����Ϊ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
��� �⣺������4����Ա�����ز�������ƽ����Ϊ$\frac{29+31+32+44}{4}=34$����������2�֣�
����4����Ա�������ļ����ȼ���ƽ���������3λͬѧ��
��������ĸ���$P=\frac{C_3^2}{C_4^2}=\frac{3}{6}=\frac{1}{2}$����4�֣�
������8������Ա��������������35���Ĺ���4�ˣ���X��ֵ����Ϊ0��1��2��3��
$P��X=0��=\frac{C_4^3C_4^0}{C_8^3}=\frac{4}{56}=\frac{1}{14}$��
$P��X=1��=\frac{C_4^2C_4^1}{C_8^3}=\frac{24}{56}=\frac{3}{7}$��
$P��X=2��=\frac{C_4^1C_4^2}{C_8^3}=\frac{24}{56}=\frac{3}{7}$��
$P��X=3��=\frac{C_4^0C_4^3}{C_8^3}=\frac{4}{56}=\frac{1}{14}$����8�֣�
��X�ķֲ���Ϊ
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{14}$ | $\frac{3}{7}$ | $\frac{3}{7}$ | $\frac{1}{14}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��м���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 Ϊ����ij������Ԥ��������Ч�������ж���ʵ�飬�õ�ͳ���������£�
Ϊ����ij������Ԥ��������Ч�������ж���ʵ�飬�õ�ͳ���������£�| δ���� | ���� | �ϼ� | |
| δע������ | 20 | x | A |
| ע������ | 30 | y | B |
| �ϼ� | 50 | 50 | 100 |
| P��X2��K0�� | 0.05 | 0.01 | 0.005 | 0.001 |
| K0 | 3.841 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����$\overrightarrow a+\overrightarrow b$��$\overrightarrow a-\overrightarrow b$��ֱ | B�� | ����$\overrightarrow a-\overrightarrow b$��$\overrightarrow a$��ֱ | ||
| C�� | ����$\overrightarrow a+\overrightarrow b$��$\overrightarrow a$��ֱ | D�� | ����$\overrightarrow a+\overrightarrow b$��$\overrightarrow a-\overrightarrow b$ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����λԲ��O��x�������ύ�ڵ�A���Ǧ���µ��ձ߷ֱ��뵥λԲ����B��xB��yB����C��xC��yC�����㣬������-��=$\frac{��}{4}$�����Ц�Ϊ��ǣ�
��ͼ����λԲ��O��x�������ύ�ڵ�A���Ǧ���µ��ձ߷ֱ��뵥λԲ����B��xB��yB����C��xC��yC�����㣬������-��=$\frac{��}{4}$�����Ц�Ϊ��ǣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ��������һ��ˮƽ�Ĺ�·����������ʻ����A��ʱ��ù�·����һɽ��D����ƫ��30��ķ����ϣ���ʻ600m��B������ô�ɽ������ƫ��75��ķ����ϣ�����Ϊ30�㣬���ɽ�ĸ߶�CD��
��ͼ��һ��������һ��ˮƽ�Ĺ�·����������ʻ����A��ʱ��ù�·����һɽ��D����ƫ��30��ķ����ϣ���ʻ600m��B������ô�ɽ������ƫ��75��ķ����ϣ�����Ϊ30�㣬���ɽ�ĸ߶�CD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com